Дифференциальное уравнение колебательного движения

Для всех трех рассмотренных случаев имеем одно и то же дифференциальное уравнение колебательного движения

.

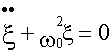Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы 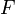, пропорциональной смещению (согласно закону Гука):

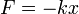
где k — положительная константа, описывающая жёсткость системы.

Если 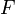— единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

4.Свободные гармонические колебания

Гармонические колебания - периодический процесс, в котором рассматриваемый параметр изменяется по гармоническому закону. Если на колебательную систему не действуют внешние переменные силы, то такие колебания называются свободными. Рассмотрим массу, которая колеблется на пружине как показано на рисунке. Если амплитуда колебаний мала, то координата x массы по вертикальной оси изменяется по гармоническому закону:

x = A sin(w t + j)

где A - амплитуда колебаний, t - время, j - фаза колебаний,w- угловая частота колебаний,w= 2 p f = 2 p / T, f - частота колебаний, T - период колебаний.

Далее мы найдём период колебаний T пружинного маятника, состоящего из грузика массой m и пружины жёсткостью k. Если грузик смещён из нулевого положения (в котором пружина не деформирована) на расстояние x, то на грузик со стороны пружины будет действовать сила- kx. Помимо этого на грузик действует сила тяжести mg. Согласно второму закону Ньютона, сумма всех сил, приложенных к грузику, равна ma, где a - ускорение. Таким образом, мы можем записать дифференциальное уравнение для пружинного маятника:

m d² x /d t ² = - kx + mg

где g - ускорение свободного падения в гравитационном поле,d² x /d t ² - вторая производная координаты x по времени t. Это уравнение имеет следующее решение:

x = A sin[(k / m)^1/2 t + j] + mg / k

Мы можем видеть из этой формулы, что период колебаний равен

T = 2p(m / k)^1/2

и, соответственно, угловая частота w равна

w = (k / m)^1/2

Уравнение свободного гармонического осциллятора с затуханием может быть записано следующим образом:

m (d² x /d t ²) + a (d x /d t) + kx = mg

где a - коэффициент трения. Это уравнение может быть переписано в виде

d² x /d t ²+ 2g(d x /d t) + W² x = g

где 2g = a / m; W²= k / m

В случае, когда W² > g² уравнение колебаний свободного гармонического осциллятора с затуханием имеет следующее решение:

x = A e^{-g t} cos(w t + j)

При этом период колебаний зависит от коэффициента затухания g:

T = 2p/w= 2p/(W² -g²)^1/2

5.Свободные гармонические колебания математического маятника

Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести 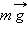уравновешивается силой натяжения нити 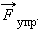При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести F _τ = – mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Рисунок 2.3.1. Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = l φ – смещение маятника по дуге

Дата добавления: 2015-04-24