Затухающие колебания пружинного маятника

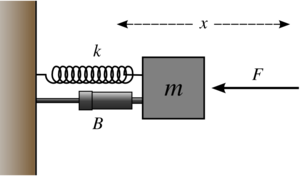
Модель пружинного маятника. B — механизм, обеспечивающий затухание. F — внешняя сила (в примере не присутствует).

Пускай имеется система, состоящая из пружины(подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).

Тогда второй закон Ньютона для рассматриваемой системы запишется так:

где F_c — сила сопротивления, F_y — сила упругости

F_c = − cv, F_y = − kx, то есть

ma + cv + kx = 0

или в дифференциальной форме

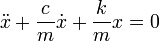
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.

Для упрощения вводятся следующие обозначения: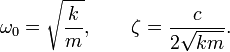

Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.

Тогда дифференциальное уравнение принимает вид

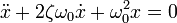
Сделав замену x = e ^{λ t} , получают характеристическое уравнение

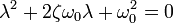
Корни которого вычисляются по следующей формуле

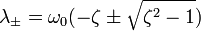
11.Характеристики затухающих колебаний: коэффициент, время релаксации, логарифмический декремент, добротность.

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением:

,

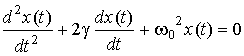Отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания:

. (7.1.9)

Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз.

ВРЕМЯ РЕЛАКСАЦИИ - характеристика процесса установления равновесия термодинамического в макроскопич. физ. системе. За В.р. 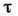отклонение к--л. параметра системы от равновесного значения уменьшается в е раз (е - основание натуральных логарифмов).

Помимо рассмотренных величин для характеристики колебательной системы употребляется величина 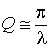, называемая добротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз. Большим значениям добротности соответствует малое затухание. Энергия колебательной системы убывает со временем. Это обусловлено наличием затухания. При малом затухании, когда энергия изменяется по закону:

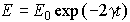, (7.1.10)

где 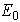- значение энергии в начальный момент.

Можно показать, что при слабом затухании добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент времени, к убыли этой энергии за один период колебаний.

11.Сложение коллинеарных гармонических колебаний равных частот.

При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой (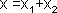) смещени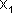й и 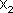, которые запишутся следующими выражениями:

, ,
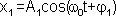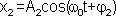Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:
= .
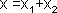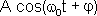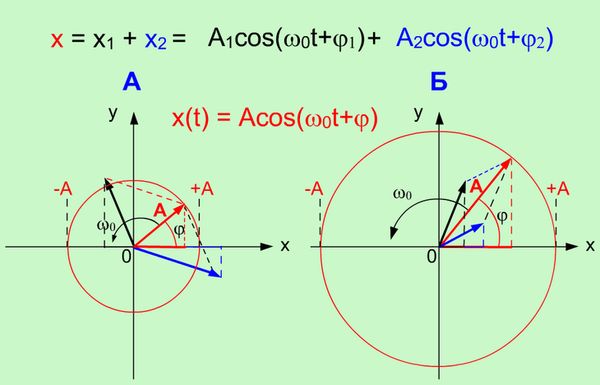
Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз (Рис. 1.2).

Рисунок 1.2. Сложение двух гармонических колебаний одинакового направления и частоты

На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм. Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний

12.Сложение коллинеарных гармонических колебаний близких частот. Биение.

сли частоты колебани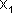й и 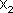, неодинаковы, векторы А1 и А2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим движение уже будет не гармоническое колебание, а сложный колебательный процесс.

Биения

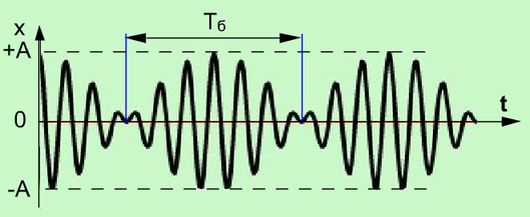
Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса (Рис 1.3.).

Рисунок 1.3. Биения

За счет того, что вращение векторов А1 и А2 происходит с близкими, но отличающимися скоростями, разность фаз этих двух колебаний будет не постоянна, а медленно, то увеличиваться, то уменьшаться. Колебания будут находиться, то в фазе, то в противофазе, в результате амплитуда суммарного сигнала тоже будет меняться. Время за которое разность фаз измениться на 2π и будет периодом биений Тб (Тб = 2π/Δω). Δω -разность круговых частот исходных колебаний.

13.Сложение ортогональных колебаний равных частот.

14. Сложение ортогональных колебаний кратных частот. Фигуры Лиссажу

Сложение ортогональных колебаний с равными частотами. Рассмотрим два векторных колебания, описываемых уравнениями:

r ₁ = A ₁·cos(w ₁·t + f₁);
r ₂ = A ₂·cos(w ₂·t + f₂).

Заметим, что с течением времени направление векторов не изменяется, а изменяется только их амплитуда. Очевидно также, что вектор A ₁параллелен r ₁, а вектор A ₂ параллелен r ₂. Задача: найти r = r ₁ + r ₂. Рассмотрим только случай взаимно-перпендикулярных колебаний (см. рис. 11.9).

Вдоль вектора r ₁ направим ось Х, вдоль r ₂ - ось Y. Очевидно, результирующий вектор r перемещается в плоскости XY. Кривая, описываемая концом вектора r, называется фигурой Лиссажу. Эта фигура вписывается в четырехугольник со сторонами 2· A ₁ и 2· A ₂, а ее вид зависит от соотношения частот, фаз и амплитуд складываемых колебаний.

Рассмотрим случай синхронных взаимно-перпендикулярных колебаний:

r ₁ = A ₁·cos (w ·t + f₁); (11.7)
r ₂ = A ₂·cos (w ·t + f₂). (11.8)

Спроецировав уравнения (11.7) и (11.8) на оси координат и проведя суммирование проекций, получим:

x = A₁·cos (w ·t + f₁); (11.9)
y = A₂·cos (w ·t + f₂). (11.10)

Исключив с помощью тригонометрических преобразований t из (11.9) и (11.10), получим математическое выражение фигуры Лиссажу, которое представляет собой уравнение эллипса:

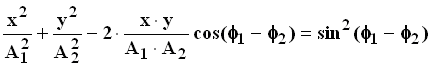. (11.11)

Вид эллипса определяется величиной сдвига фаз Df. В общем случае, когдаDf отлична от 0, полуоси эллипса повернуты относительно осей X и Y.

Если сдвиг фаз Df = 0, то как следует из уравнения (11.11) будет справедливо следующее выражение:

(х/А₁ - y/A₂)² = 0 или
y = А₂·x/А₁.

Т.е. фигура Лиссажу представляет из себя прямую линию с углом наклона aк оси X (tg a = А₂/А₁). Если Df = p, то y = - А₂·x/А₁.

Если Df = p/2, то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат:

х²/А₁² + y²/A₂² = 1.

Если Df = p/2 и А₁ = А₂ = A, то эллипс превращается в окружность радиусаA.

Дата добавления: 2015-04-24