Характеристиками гармонических колебаний являются: смещение, амплитуда,период, частота, циклическая частота, фаза, начальная фаза

Колеблющееся тело всегда связано с другими телами и вместе с ними образует колебательную систему. Если колебательная система не подвергается переменным внешним воздействиям, то колебания, возникающие вследствие какого-либо отклонения этой системы от состояния устойчивого равновесия, называют свободными (собственными). Если идеальную колебательную систему вывести из положения равновесия, а затем предоставить самой себе, то в ней возникнут свободные колебания.

Колебаниями называют процессы, многократно повторяющиеся через определенный промежуток времени. Колебания бывают периодическими инепериодическими. Непериодические колебания можно разложить напериодические составляющие. Если возврат к положению равновесия совершается через равные промежутки времени, то такие колебания называются периодическими.

Свободные колебания в идеальных колебательных системах называются гармоническими. Они отвечают следующим требованиям:

а) максимальные отклонения колеблющегося тела в одну и другую сторону от положения равновесия равны;
б) время отклонения в одну сторону равно времени отклонения в другую сторону;
в) характер движения тела в обе стороны от положения равновесия одинаков;
г) колебания продолжаются бесконечно долго.

Свободные гармонические колебания совершаются телом под действием силы, пропорциональной смещению и направленной к положению равновесия: F_x = –kx,

2.Гармонические колебания. Основные параметры.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

x (t) = A sin(ω t + φ)

или

x (t) = A cos(ω t + φ),

Графики функций f (x) = sin(x) и g (x) = cos(x) на декартовой плоскости.

где х — значение изменяющейся величины, t — время, остальные параметры - постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний,(ω t + φ) — полная фаза колебаний, 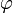— начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

§ Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).

§ Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (т.е. чтобы зависимость от времени этой силы была синусоидальной).

3.Дифференциальное уравнение гармонических колебаний. Понятие о гармоническом осцилляторе

Дата добавления: 2015-04-24