Показательное распределение непрерывной случайной величины

26.

23.

22.

24.Числовые характеристики непрерывной случайной величины.
Математическим ожиданием непрерывной случайной величины , возможные значения которой принадлежат отрезку 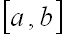, называют определенный интеграл
.
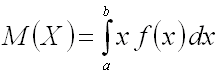Если возможные значения принадлежат всей числовой оси, то

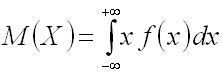
(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные непрерывной случайной величины принадлежат отрезку 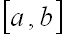, то
.
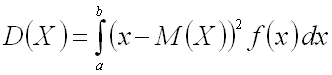Если возможные значения принадлежат всей числовой оси, то

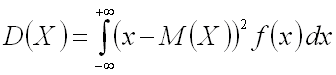
(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).
Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:
.

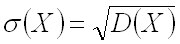25.Равномерное распределение непрерывной случайной величины.

Равномерное распределение. Непрерывная величина Х распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:

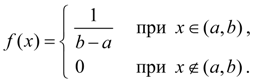(29)

Для случайной величины Х, равномерно распределенной в интервале (a, b) (рис. 4), вероятность попадания в любой интервал (x 1, x 2), лежащий внутри интервала (a, b), равна:

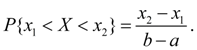(30)

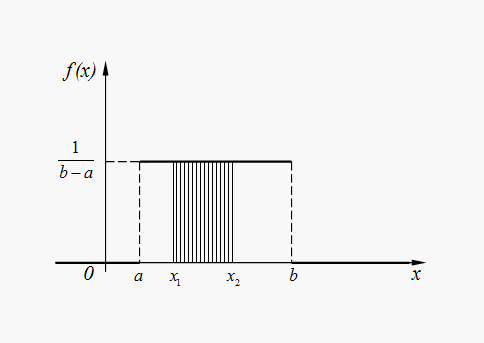
Рис. 4. График плотности равномерного распределения

Примерами равномерно распределенных величин являются ошибки округления. Так, если все табличные значения некоторой функции округлены до одного и того же разряда 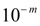, то выбирая наугад табличное значение, мы считаем, что ошибка округления выбранного числа есть случайная величина, равномерно распределенная в интервале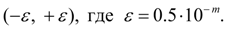

Непрерывная случайная величина Х, функция плотности которой задается выражением

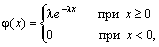
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение. Здесь параметр λ постоянная положительная величина.
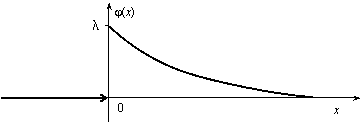
Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Также этому распределению подчиняется время ожидания клиента в системе массового обслуживания (магазин, мастерская, банк, парикмахерская и т.д.). Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению. График дифференциальной функции показательного распределения показан на рис. 2.11.

35.

28,

29,

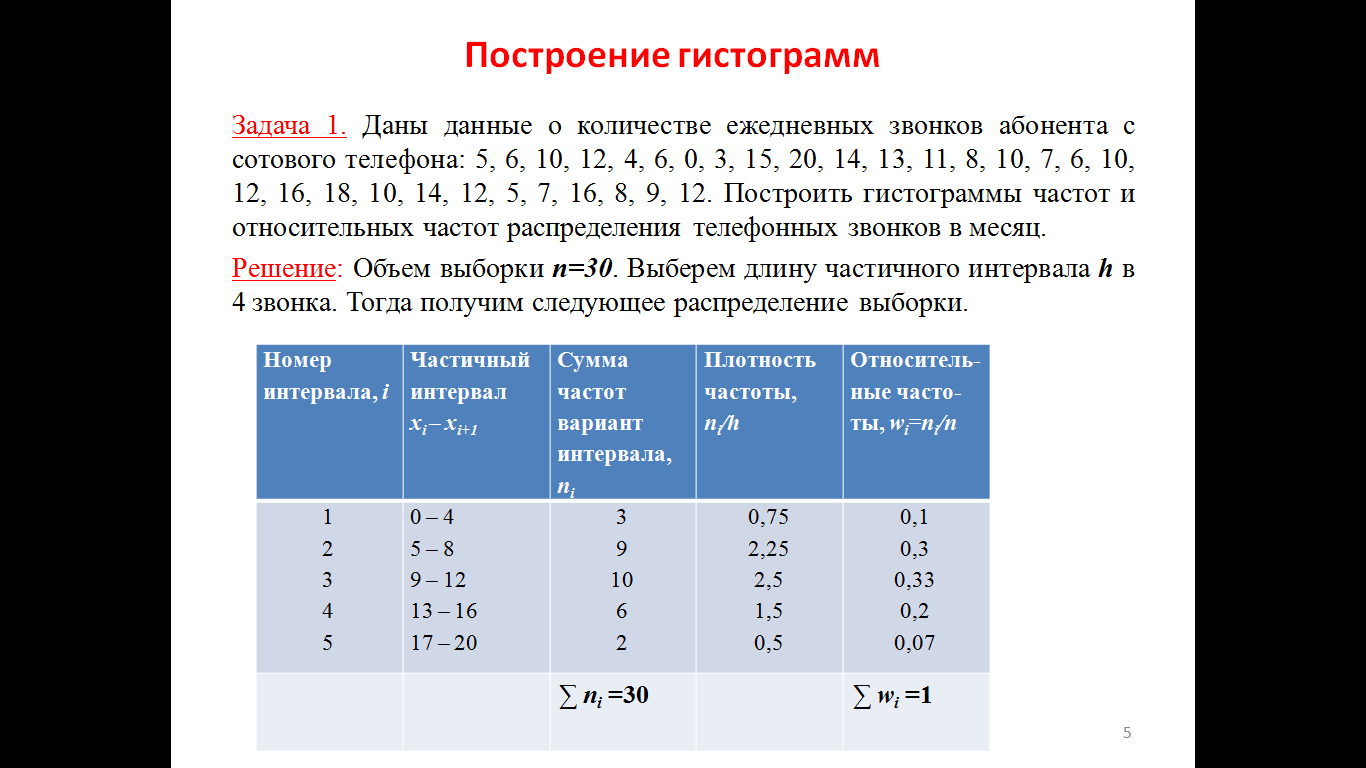
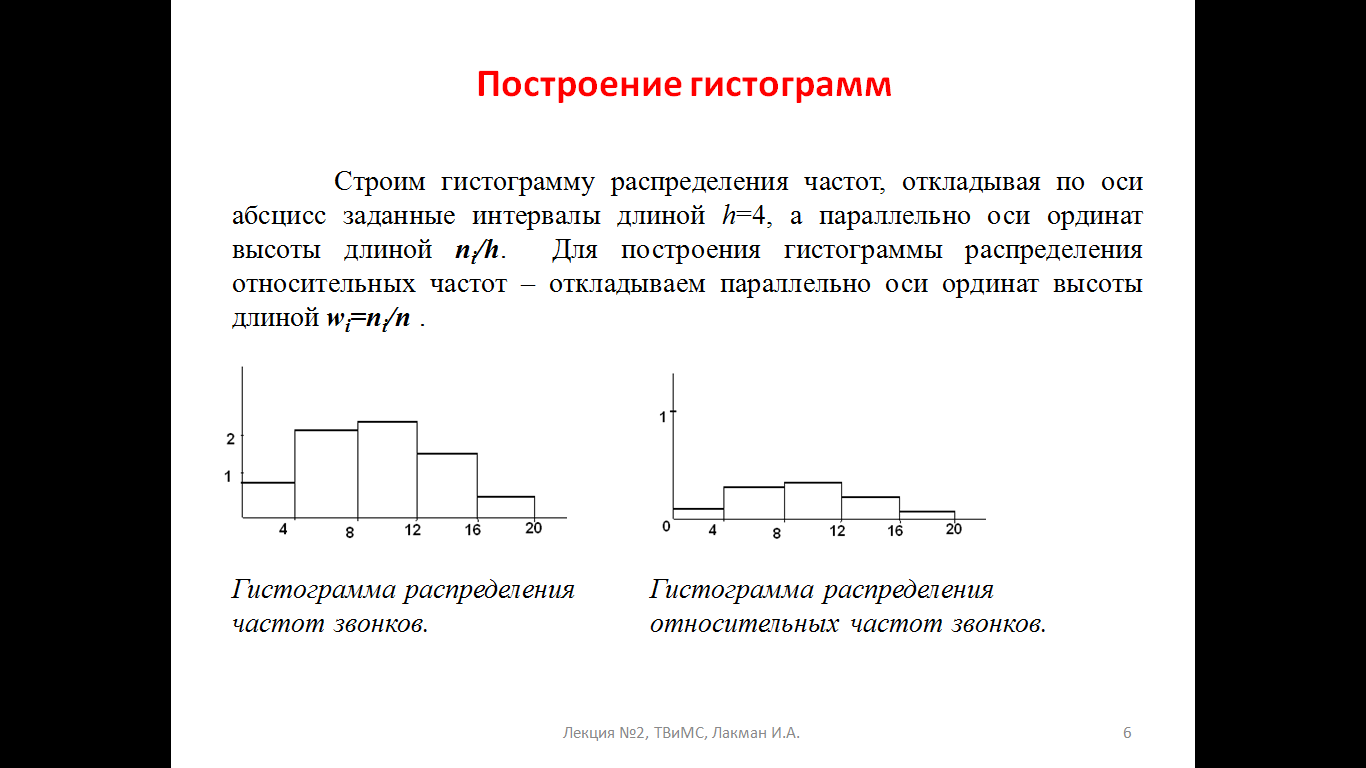
33,

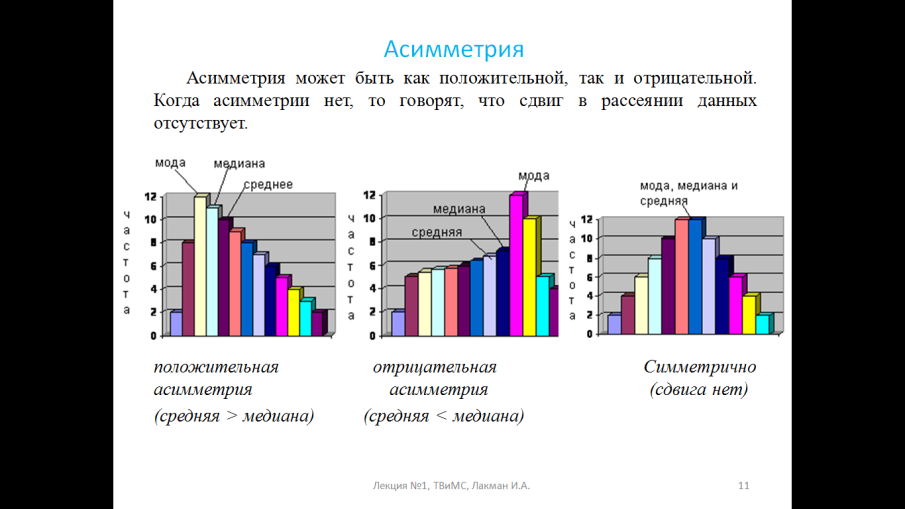
34,

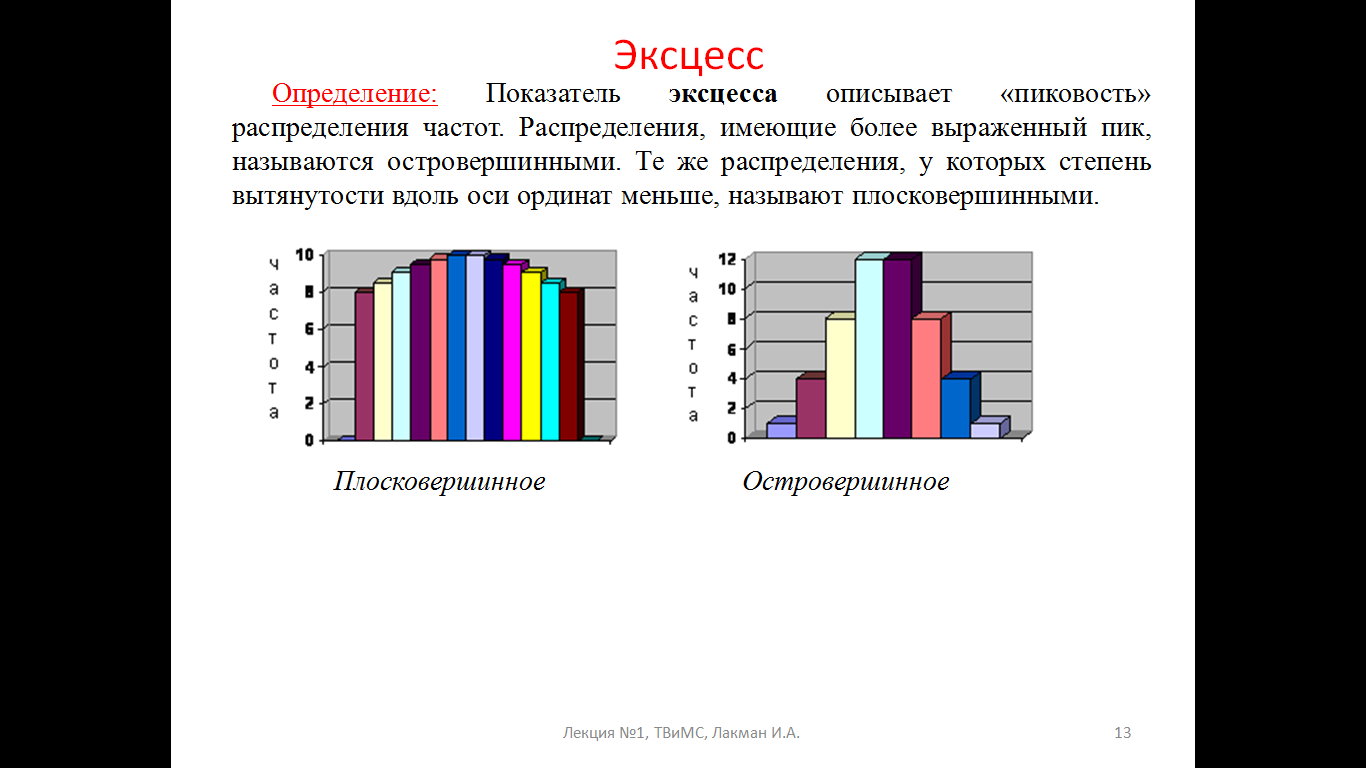
37,

39,

40,

42,

41,

43,

51,

52,

Дата добавления: 2015-04-24