Показатели тесноты связи

Показатели тесноты связи дают возможность охарактеризовать зависимость вариации результативного признака от вариации признака-фактора.
Более совершенным показателем степени тесноты корреляционной связи являетсялинейный коэффициент корреляции. При расчете этого показателя учитываются не только отклонения индивидуальных значений признака от средней, но и сама величина этих отклонений.

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy, который можно рассчитать по следующим формулам:

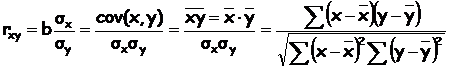
Линейный коэффициент корреляции находится в пределах: -1£rxy£1.

Если r>0, то прямая связь

Если r<0, то обратная связь

Если |r|³0,7, то сильная связь

Если 0,5£|r|<0,7, то умеренная связь

Если |r|<0,5, то слабая связь

Если b>0, то 0£rxy£1, если b<0, то -1£rxy£0.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 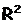, называемый коэффициентом детерминации. Коэффициент детерминации показывает сколько процентов приходится на долю учтенных в модели факторов:

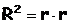
Соответственно величина 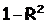характеризует долю дисперсии y, вызванную влиянием остальных, не учтенных в модели, факторов.

Тесноту связи между признаками x и y оценивают посредством таких показателей: коэффициент Фехнера; коэффициент корреляции рангов Спирмена; линейный коэффициент корреляции и др.

1. 
   ^ Коэффициент Фехнера:

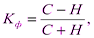
где 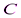– число совпадений знаков отклонений индивидуальных значений факторного признака х и результативного признака у от соответствующих средних величин 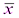и ;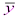

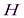– число несовпадений знаков отклонений индивидуальных значений факторного признака х и результативного признака у от соответствующих средних величин 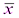и .

1. 
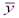   Коэффициент корреляции рангов Спирмена:

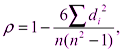
где 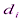– разность между рангами факторного и результативного признаков ();

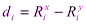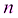– число единиц изучаемого ряда.

1. 
   Линейный коэффициент корреляции:

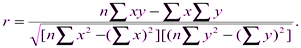
Представленные выше коэффициенты могут принимать значения от –1 до +1. Отрицательные значения коэффициентов указывают на обратную корреляционную связь, положительные – на прямую. Чем ближе коэффициенты по абсолютной величине к 1, тем теснее связь между признаками, и наоборот, чем ближе коэффициенты к 0, тем слабее связь.

Дата добавления: 2015-04-24