Расчет параметров линейной парной регрессии

Регрессионный анализ, его цель и назначение

Общее представление о корреляционно-регрессивном анализе

Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. Предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов. Рассмотрим метод корреляционно-регрессионного анализа, который является основным в изучении взаимосвязей явлений.

Данный метод содержит две свои составляющие части — корреляционный анализ и регрессионный анализ. Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.

Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0. Она используется далее в примерах по теме.

Регрессионный анализ — это статистический метод исследования зависимости случайной величины у от переменных (аргументов) хj (j = 1, 2,..., k),рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения xj.

Обычно предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием 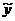= φ(x1,..., хk),являющимся функцией от аргументов хj и с постоянной, не зависящей от аргументов дисперсией σ2.

Для проведения регрессионного анализа из (k + 1)-мерной генеральной совокупности (у, x1, х2,..., хj,..., хk) берется выборка объемом n, и каждое i-е наблюдение (объект) характеризуется значениями переменных (уi, xi1, хi2,..., хij,..., xik), где хij — значение j-й переменной для i-го наблюдения (i = 1, 2,..., n), уi— значение результативного признака для i-го наблюдения.

Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид

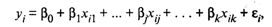(53.8)

где βj — параметры регрессионной модели;

εj — случайные ошибки наблюдения, не зависимые друг от друга, имеют нулевую среднюю и дисперсию σ2.

Отметим, что модель (53.8) справедлива для всех i = 1,2,..., n, линейна относительно неизвестных параметров β0, β1,…, βj, …, βk и аргументов.

Как следует из (53.8), коэффициент регрессии Bj показывает, на какую величину в среднем изменится результативный признак у, если переменную хjувеличить на единицу измерения, т.е. является нормативным коэффициентом.

В матричной форме регрессионная модель имеет вид

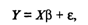(53.9)

где Y — случайный вектор-столбец размерности п х 1 наблюдаемых значений результативного признака (у1, у2,.... уn); Х— матрица размерности п х (k + 1) наблюдаемых значений аргументов, элемент матрицы х,, рассматривается как неслучайная величина (i = 1, 2,..., n; j=0,1,..., k; x0i, = 1); β — вектор-столбец размерности (k + 1) х 1 неизвестных, подлежащих оценке параметров модели (коэффициентов регрессии); ε — случайный вектор-столбец размерности п х 1 ошибок наблюдений (остатков). Компоненты вектора εi не зависимы друг от друга, имеют нормальный закон распределения с нулевым математическим ожиданием (Mεi = 0) и неизвестной постоянной σ2 (Dεi = σ2).

На практике рекомендуется, чтобы значение п превышало k не менее чем в три раза.

парная - регрессия между двумя переменными у и x, т. е, модель вида: у = f (x) + Е, где у -зависимая переменная (результативный признак), x – независимая, объясняющая переменная (признак - фактор), Е - возмущение, или стохастическая переменная, включающая влияние неучтенных факторов в модели.

В случае парной линейной зависимости строится регрессионная модель по уравнению линейной регрессии. Параметры этого уравнения оцениваются с помощью процедур, наибольшее распространение получил метод наименьших квадратов.

Метод наименьших квадратов (МНК) - метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.

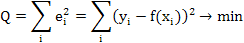
где у_i- статические значения зависимой переменной; f (х) - теоретические значения зависимой переменной, рассчитанные с помощью уравнения регрессии.

Экономический смысл параметров уравнения линейной парной регрессии. Параметр b показывает среднее изменение результата у с изменением фактора х на единицу. Параметр а = у, когда х = 0. Если х не может быть равен 0, то а не имеет экономического смысла. Интерпретировать можно только знак при а: если а > 0. то относительное изменение результата происходит медленнее, чем изменение фактора, т. е. вариация результата меньше вариации фактора: V < V. и наоборот.

То есть МНК заключается в том, чтобы определить а и а, так, чтобы сумма квадратов разностей фак­тических у и у. вычисленных по этим значениям a₀ и а1 была минимальной:

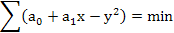
Рассматривая эту сумму как функцию a₀ и a₁дифференцируем ее по этим параметрам и приравниваем производные к нулю, получаем следующие равенства:

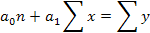
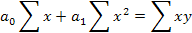
n - число единиц совокупности (заданны параметров значений x и у). Это система «нормальных» уравнений МНК для линейной функции (y_x)

Расчет параметров уравнения линейной регрессии:

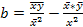, a = y – bx

Нахождение уравнения регрессии по сгруппированным данным. Если совокупность сгруппирована по признаку x, для каждой группы найдены средние значения другого признака у, то эти средние дают представление о том, как меняется в среднем у в зависимости от х. Поэтому группировка служит средством анализа связи в статистике. Но ряд групповых средних у_x имеет тот недостаток, что он подвержен случайным колебаниям. Они создают колебания у_x отражающие не закономерность данной зависимости, а затушевывающий ее «шум».

Групповые средние хуже отражают закономерность связи, чем уравнение регрессии, но могут быть использованы в качестве основы для нахождения этого уравнения. Умножая численность каждой группы n_ч на групповую среднюю уч мы получим сумму у в пределах группы Суммируя эти суммы, найдем общую сумму у. Несколько сложнее с суммой ху. Если при сумме ху интервалы группировки малы, то можно считать значение x для всех единиц в рамках группы одинаковым Умножив на него суммуу, получим сумму произведений x на у в рамках группы и, суммируя эти суммы, общую суммуxу. Численность n_x, здесь играет такую же роль, как взвешивание в вычислении средних.

С помощью регрессионного анализа формируется модель или форма связи между факторами и результативными признаками. Если модель отражает связь между одним факторным и результативным показателем, то модель назыв.прогрессивной. Результативный показатель – ŷ; ŷ = ао + а1*х - уравнение линейной парной регрессии ао, а1 – параметры; х=0, ŷ= ао; а1 – опред.силу связи между фак-ым и результ-ым показателем. Линейная 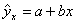; Гиперболическая 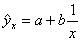; Параболическая 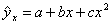; Показательная 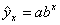; ; 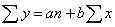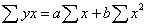. Для проверки возможности использования линейной функции определяется разность 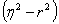, если она <0,1 то можно применить линейную функцию. 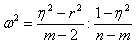,m – число групп. Если 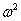< F-критерия, то можно. (Значение F-критерия определяется по таблице α=0,05, число степеней свободы числителя (k1 = m-2) и знаменателя (k2 =n-m))

Дата добавления: 2015-04-24