Линейный коэффициент корреляции

Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Виды зависимостей:

1) парная корреляция – связь между двумя признаками (между двумя факторными либо между факторным и результативным признаком)

2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков

3) множественная корреляция – зависимость результативного и двух и более факторных признаков.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками.

Теснота связи количественно выражается величиной коэффициентов корреляции.

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:

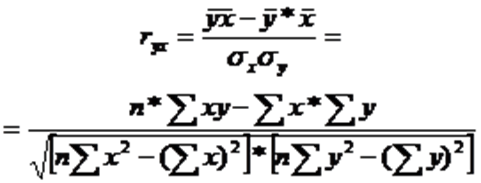
Линейный коэффициент корреляции изменяется в пределах от -1 до+1.

По степени тесноты связи различают количественные критерии оценки тесноты связи:

Величина коэффициента корреляции	Характер связи
До ±0,3	Практически отсутствует
±0,3 – ±0,5	Слабая
±0,5 – ±0,7	Умеренная
±0,7 – ±1,0	Сильная

Наиболее распространенный коэффициент корреляции. Предназначен для расчета силы и направления линейной зависимости между переменными исследования.

Смысл коэффициента линейной корреляции.

Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной шкале либо в шкале отношений.

Если представить две переменные на координатном поле, то каждая пара значений будет отображать координаты точки в этом поле. Чем ближе точки к усредненной прямой, тем выше коэффициент корреляции (см. следующий рисунок),.

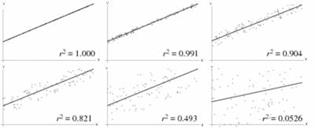
Коэффициент корреляции будет положительным числом, когда при повышении X происходит повышение Y(прямопропорциональная связь), отрицательным при обратнопропорциональной связи. На иллюстрации изображены различные по силе положительные коэффициенты корреляции.

На следующей иллюстрации видны специально сгенерированные формы зависимостей и коэффициенты корреляции для них.

Как видим, линейный коэффициент корреляции срабатывает лишь при линейном характере взаимосвязи переменных.

Формула

Общая формула:

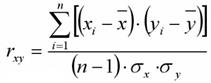
Где x_i и y_i - сравниваемые количественные признаки, n – число сравниваемых наблюдений, σ_x и σ_y – стандартные отклонения в сопоставляемых рядах.

Для расчетов вручную используется преобразованная формула:

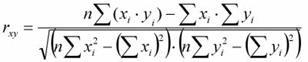
Несмотря на кажущуюся громоздкость формулы, она значительно облегчает ручной расчет.

Для расчетов в Excel используется функция ПИРСОН.

Иллюстрация расчетов:

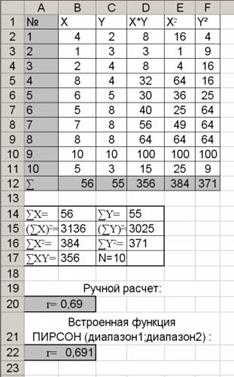
Полученный коэффициент корреляции проверяется на значимость с помощью таблицы критических значений. Для этоговычисляем количество степеней свободы df=N-2 и на пересечении с необходимым уровнем значимости находим критическое значение коэффициента.

В нашем случае df=8, уровень значимости выбираем 0,1. Получаем критический коэффициент r=0.54. Так как 0,69 > 0,54 делаем вывод о значимой корреляции (r=0,69;p≤0,1).

Дата добавления: 2015-04-24