Пример 1. Вычисление моды и медианы в интервальном вариационном ряду

Вычисление моды и медианы в интервальном вариационном ряду

Мода в интервальном вариационном ряду вычисляется по формуле

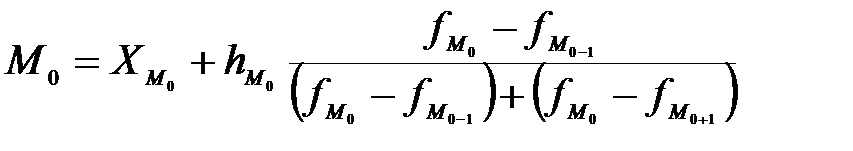
где Х_М0 - начальная граница модального интервала,

hм₀ – величина модального интервала,

fм₀, fм_0-1, fм₀₊₁ – частота соответственно модального интервала, предшествующего модальному и последующего.

Модальным называется такой интервал, которому соответствует наибольшая частота.

Группы по стажу	Число рабочих, чел	Накопленные частоты
До 2
2-4
4-6
6-8	35	82
8-10
свыше 10
ИТОГО:		-

Определить моду и медиану.

Решение.

Модальный интервал [6-8], т.к. ему соответствует наибольшая частота f = 35. Тогда:

Хм₀ =6, fм₀ =35

hм₀ =2, fм_0-1 =20

fм₀₊₁ =11

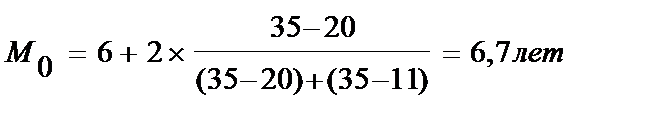
Вывод: Наибольшее число рабочих имеет стаж примерно 6,7 лет.

Для интервального ряда Ме вычисляется по следующей формуле:

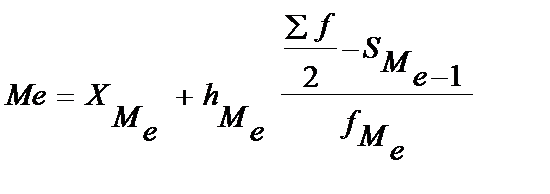
где Хм_е – нижняя граница медиального интервала,

hм_е – величина медиального интервала,

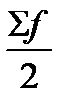– половина суммы частот,

fм_е – частота медианного интервала,

Sм_е-1 –сумма накопленных частот интервала, предшествующего медианному.

Медианный интервал – такой интервал, которому соответствует кумулятивная частота, равная или превышающая половину суммы частот.

Определим медиану для нашего примера.

Найдем:

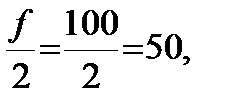
т.к 82>50, то медианный интервал [6-8].

Тогда:

Хм_е =6, fм_е =35,

hм_е =2, Sм_е-1 =47,

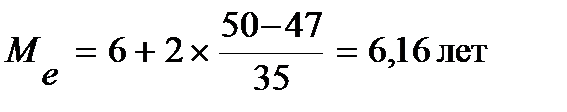
Вывод: Половина рабочих имеет стаж меньше 6,16 лет, а половина имеет стаж больше, чем 6,16 лет.

25 Характеристика показателей вариации. Средняя величина, характеризуя вариационный ряд в целом, не показывает, как располагаются вокруг нее варианты осредняемого признака, т.е. средняя не характеризует колеблемость признака. Однако именно колеблемость признака позволяет нам судить о равномерности того или иного процесса или явления или об однородности изучаемой совокупности, а значит и о надежности средних величин.

Пример вычисления средних в двух вариационных рядах с разным распределением частот:

x	f	xf	x	f	xf
ИТОГО:

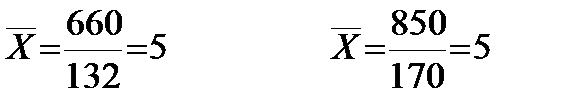
Для 1-го ряда не более, чем на 1 от среднего значения отклоняется 120 единиц (30+60+30), или 91% (120/132 · 100%) всех единиц совокупности.

Для 2-го ряда не более, чем на 1 от среднего значения отклоняется 70 (10+10+50), или 42% (70/850 · 100%) всех единиц совокупности.

Вывод: 1-ый ряд является более однородным, чем 2-ой, и средняя характеристика для него более надежна.

Задача статистики заключается в том, чтобы дать числовое выражение колеблемости признака для более глубокого понимания сущности изучаемых явлений. Для этого в статистике рассчитываются следующие показатели вариации:

– размах вариации (R);

– среднее линейное отклонение ();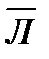

– дисперсия (σ²);

– среднее квадратическое отклонение (σ).

Кроме них используют относительный показатель вариации – коэффициент вариации (V).

Размах вариации R вычисляется по формуле

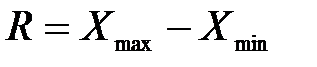
где X_maх (Х_min) – самое большое (малое) значение, принимаемое единицей совокупности.

Этот показатель является очень приблизительным, т.к. учитывает лишь значения крайних единиц совокупности. Поэтому его применяют редко, лишь в тех случаях, когда особые значения имеют либо наибольшее, либо наименьшее значения варианты.

Стремление составить показатель вариации, который учитывал бы все значения вариант, приводит к среднему линейному отклонению – это средняя арифметическая из абсолютных значений отклонений вариант от их средней арифметической. Применяется в 2 формах:

– простой:

;

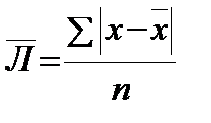– взвешенной:

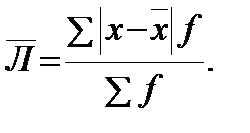
Недостатком этого показателя является то, что он не учитывает знаков отклонений.

Чтобы усилить различия в величинах отклонений, эти отклонения возводятся в квадрат, тогда отклонения меньше 1 уменьшаются, а больше 1- увеличиваются, и вводят новый показатель вариации – дисперсию. Это средний квадрат отклонения вариант от их средней арифметической. Используется в двух формах:

– простой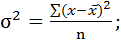

– взвешенной: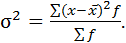

Среднее квадратическое отклонение (σ):

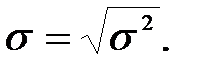
Рассмотренные показатели относятся к абсолютным показателям вариации и6 измеряются в тех же единицах, что и варианты (дисперсия – в квадратных единицах). Это не позволяет сравнивать между собой различные совокупности. Для этого вводится относительный показатель вариации, который называется коэффициентом вариации – это отношение среднего квадратического отклонения к средней арифметической: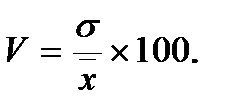

Чем большее значение принимают показатели вариации, тем менее однородна совокупность и тем менее надежна средняя.

Принято считать, что если V >40%, то это свидетельствуют о большой колеблемости признака в изучаемой совокупности. В этом случае среднее значение ненадежно, недостоверно и по нему нельзя судить обо всей совокупности.

Дата добавления: 2015-04-24