Измерение тесноты связи между количественными признаками

Коэффициенты ассоциации и контингенции

Коэффициенты ассоциации и контингенции применяются тогда, когда исследуется связь между варьированием двух атрибутивных признаков, по каждому признаку имеется две группы (таблица 10.2).

Таблица 10.2 – Варьируемые атрибутивные признаки

			Всего
	a	B	a+b
	c	D	c+d
Итого	a+c	b+d	a+b+c+d

Коэффициент ассоциации вычисляется по формуле

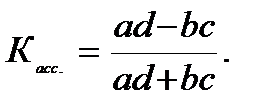
Коэффициент контингенции вычисляется

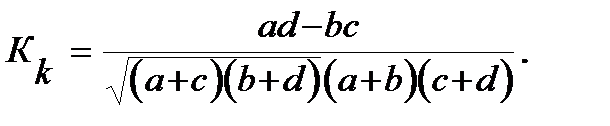
Коэффициенты контингенции и ассоциации принимают значение от -1 до 1, показывают не только тесноту, но и направление связи.

Если коэффициент >0, связь прямая, <0 – обратная. Чем ближе коэффициент к ±1, тем связь теснее.

Коэффициент контингенции всегда меньше коэффициента ассоциации. Он дает более осторожную оценку тесноты связи.

Методы измерения связи между количественными признаками не могут обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических (корреляционных и дисперсионных). 55 Измерение тесноты связи между признаками

Для определения тесноты связи между факторным и результативным признаком используются:

1 индекс корреляции R, вычисляемый по формуле

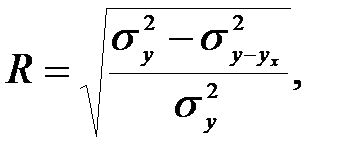
где 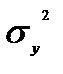− общая дисперсия,

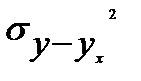− дисперсия, измеряющая отклонение y от y_x .

Значение R меняется от 0 до 1. Чем ближе к 1, тем связь теснее. Применяется для любого вида связи (не показывает направления).

2 теоретическое корреляционное отношение η:

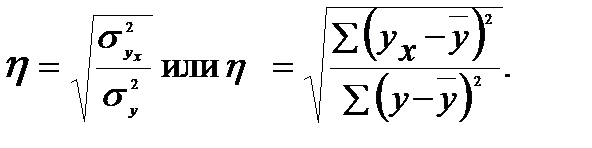
Частным случаем теоретического корреляционного отношения является линейный коэффициент корреляции (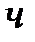), который применяется только в случае линейной связи. Он меняется от −1 до 1, показывает не только тесноту, но и направление связи. Вычисляется по следующей формуле:

.

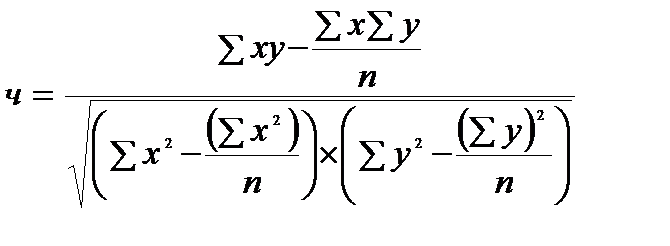56 Метод сравнения параллельных рядов Установить наличие и характер связи между количественными признаками можно с помощью метода сравнения параллельных рядов, заключающегося в следующем.

Признаки-факторы мы располагаем в возрастающем или убывающем порядке в зависимости от целей исследования и рядом записываем соответствующий результативный признак. Затем путем сопоставления двух параллельных рядов делаем предположение о наличии связи и ее направлении. Пример 1 Находим зависимость между производительностью труда (у) и энерговооруженностью (х), имея данные по 25-и заводам.

№ завода	Х	У	Знаки отклонений	Ранги	Разность рангов
Х	У	Х	У	│d│	d^2
	6,0		-	-		1,5	0,5	0,25
	6,1		-	-		3,5	1,5	2,25
	6,8		-	-		10,5	7,5	56,25
	7,2		-	-		5,5	1,5	2,25
	7,4		-	-		1,5	3,5	12,25
	7,9		-	-		3,5	2,5	6,25
	8,2		-	-		5,5	1,5	2,25
	8,5		-	-		7,5	0,5	0,25
	8,6		-	-		10,5	1,5	2,25
	9,1		-	+		17,5	7,5	56,25
	9,4		-	-		7,5	3,5	12,25
	9,9		-	+		14,0	2,0	4,00
	10,5		+	+		14,0	1,0	1,00
	11,2		+	+		17,5	3,5	12,25
	11,3		+	-		10,5	4,5	20,25
	11,5		+	+		21,5	5,5	30,25
	11,7		+	+		21,5	4,5	20,25
	12,1		+	+		17,5	0,5	0,25
	12,3		+	+		14,0	5,0	25,00
	12,6		+	+		17,5	2,5	6,25
	12,7		+	+		21,5	0,5	0,25
	12,9		+	-		10,5	11,5	132,25
	13,0		+	+		24,5	1,5	2,25
	13,2		+	+		21,5	2,5	6,25
	13,3		+	+		24,5	0,5	0,25
Итого:	253,7		–	–	–	–	–	413,50

Дата добавления: 2015-04-24