Виды средних и методы их расчета. Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку

Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя.

основные условия расчета и применение средних величин:

1. расчет надо вести для однородной, однокачественной совокупности,

2. общие средние необходимо дополнить групповыми средними и индивидуальными

величинами,

3. совокупность для расчета средних должна быть достаточно велика min - 20-

30 единиц.

4. необходимо правильно выбрать единицу совокупности для расчета средних.

Все виды средних делятся на:

· степенные (аналитические, порядковые) средние (арифметическая, гармоническая, геометрическая, квадратическая);

· структурные (позиционные) средние (мода и медиана) — применяются для изучения структуры рядов распределения.

Различают следующие виды средней, каждая из которых может быть простой и взвешенной:

1)Средняя арифметическая простая (не взвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

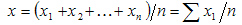
Средняя арифметическая взвешенная. При расчете средних величин отдельные значения признака могут повторяться, встречаться по нескольку раз. В данном случае расчет проводится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

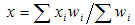
признака. Различают среднюю гармоническую простую и взвешенную.

Средняя гармоническая простая.

Средняя гармоническая взвешенная применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.

Средняя арифметическая и средняя гармоническая величины могут применятся в одних и тех же ситуациях, но по разным данным. Если в ИСС неизвестен числитель, то в расчетах применяется средняя арифметическая величина. Если в ИСС неизвестен знаменатель, то в расчетах используется средняя гармоническая величина.

3)Средняя квадратическая величина применяется тогда, когда вместо индивидуальных значений признака представлены квадраты исходных величин.

4)Средняя геометрическая применяется в случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям.

5)Средняя степенная. В математической статистике различные средние выводятся из формул степенной средней:

Средние относятся к классу степенных средних.

Xcp= ((Sxm)/n)1/m

если m=1 - средняя арифметическая,

если m=-1 - средняя гармоническая,

если m=2 - средняя квадратическая,

если m=0 - средняя геометрическая,

среднее хронологическое, структурное среднее (мода, медиана)

Любая средняя величина исчисляется из экономического содержания показателей.

Средняя себестоимость Zcp=SZq/Sq, где q - сумма всей продукции

Среднее арифметическое и гармоническое наиболее часто применяется для расчета

обобщающих показателей.

Средняя арифметическая простая xcp=Sx/n

Средняя арифметическая взвешенная xcp=Sx*f/Sf, где f - частота встречаемости

Средняя гармоническая простая xcp=n/S(1/x)

Средняя гармоническая взвешенная xcp=SM/S(M*(1/x)); M=x*f

Средняя квадратическая простая xcp=((Sx2)/n)1/2

Средняя квадратическая взвешенная xcp=((Sx2*f)/Sf)1/2

применяется только при исчислении показателей вариации

Средняя геометрическая xcp=(x1m*x2

m*...*xnm)1/m xcp=(Пx)

1/m используется в рядах динамики

Среднее хронологическая - используется для моментальных рядов

xcp=(1/2x1+x2+x3+...+1/2xn)/n-1

Мода - это варианта с наибольшей частотой. Медианта

- это варианта, которая лежит в середине ряда распределения и делит совокупность

пополам.

Правило выбора средней:

средняя арифметическая применяется тогда когда имеются варианты и абсолютное

число единиц вариантов и их удельный вес. Средняя гармоническая применяется

когда имеются варианты, а в качестве веса - производная величина. Выбор вида

средней зависит от исходной информации.

Дата добавления: 2015-04-24