Сопряженное пространство. Теорема о полноте сопряженного пространства

Слабая компактность шара в сопряженном пространстве. Теорема о вложенных шарах (с док-ом).

Операторы с чисто точечным спектром. Теорема о связи с собственными значениями (с док-ом).

Интегральные уравнения Фредгольма. Случай вырожденных ядер.

Интегральные уравнения с вырожденным ядром. Методика решения интегральных уравнений с вырожденным ядром.

Сопряженные, самосопряженные и унитарные операторы в Гильбертовых пространствах.

Пусть L - линейное пространство над полем P.

Линейным функционалом на пространстве L называется отображение 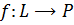, обладающее свойством: , где

Обозначим через множество всех линейных функционалов на L.

Определим операции сложения и умножения на числа по формулам:

1)

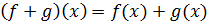
2)

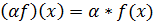
Таким образом, на множестве вводится структура линейного пространства. Это линейное пространство называется сопряженным пространством для пространства L.

Теорема о полноте сопряженного пространства

Дата добавления: 2015-04-24