Сложение гармонических колебаний одинаковой частоты и направления. Векторная диаграмма

Действие периодической силы на затухающий гармонический осциллятор. Резонанс.

Гармонический осциллятор — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x:

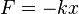, где k — коэффициент жёсткости системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором.

Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.

На практике часто приходится иметь дело с колебаниями одинаковой частоты. Любые два таких колебания можно представить в виде:

y₁ = A₁ sin (ωt + φ₁); y₂ = A₂ sin (ωt + φ₂).

Особый интерес представляет случай, когда начальная фаза первого колебания равна 0, а начальная фаза второго колебания равна ^π/₂.
Тогда y₁ = A₁ sin ωt; y₂ = A₂ sin (ωt + ^π/₂). Сумма таких гармонических колебаний равна:

A₁ sin ωt + A₂ cos ωt = 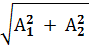• sin (ωt + ) (1)

где угол φ определяется из условий

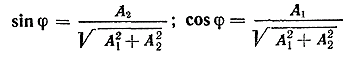(2)

Формула A₁ sin ωt + A₂ cos ωt = 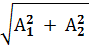• sin (ωt + ) показывает, что если два гармонических колебания имеют одинаковую частоту и фазы 0 и ^π/₂, то их сумма есть гармоническое колебание той же частоты.

Возможны случаи, когда тело участвует в двух и более колебаниях, которые

происходят вдоль одного или разных направлений. Рассмотрим сложение двух гармонических колебаний одинакового направления и частоты, которые происходят с некоторой разностью фаз и имеют разные амплитуды. Смещение x от положения равновесия колеблющегося тела будет равно сумме смещений x₁ и x₂:

x₁=A₁cos(ωₒt+αₒ₁),

x₂=A₂cos(ωₒt+αₒ₂).

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов.

Дата добавления: 2015-04-24