Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством)

Определители матриц, их свойства (доказать для определителя второго порядка).

Энтропия и вероятность. Формула Больцмана. Макро- и микросостояния. Термодинамическая вероятность макросостояния (статистический вес).

Энтропия встатистической физике — мера вероятности осуществления какого-либо макроскопического состояния

S=k*ln(P), k = R/N = 1,38*10^-23 Дж/К,(1)

где k - фундаментальная мировая постоянная Больцмана;
R = 8,31 Дж/(моль*К) - молярная газовая постоянная;
N = 6,06*10²³ моль^-1 - число Авогадро;
Р - статистический вес: число способов осуществления данного состояния.

Представим формулу (1) в виде: P = e^S/K

и обратим внимание на то, что статистический вес состояния системы P экспоненциально растет с ростом S. Иными словами, менее упорядоченное состояние (больший хаос) имеет больший статистический вес ^*, т. к. оно может быть реализовано большим числом способов. Следовательно, энтропия - мера неупорядоченности системы.

Из-за случайных перекладываний растет беспорядок на столе, в комнате. Порядок создается искусственно, беспорядок - самопроизвольно, т. к. ему отвечает большая вероятность, большая энтропия. Разумная деятельность человека направлена на преодоление разупорядоченности.

МИКРОСКОПИЧЕСКОЕ СОСТОЯНИЕ (микросостояние) системы - определяется в классической механике заданием координат и импульсов всех частиц системы.
МАКРОСКОПИЧЕСКОЕ СОСТОЯНИЕ (макросостояние) системы - определяется значениями ее термодинамических параметров: давления p, температуры Т, удельного объема v, внутренней энергии U и т. п. Для определения макроскопического состояния однокомпонентной системы достаточно знать значения любых 2 независимых параметров (напр., Т и p или Т и v).

Статистический вес состояния системы - это число способов, которыми может быть реализовано данное состояние системы. Статистические веса всех возможных состояний системы определяют её энтропию.

Свойства:

1. Определитель транспонированной матрицы равен определителю исходной матрицы

2. Если в определителе какие-либо две строки (столбца) равны между собой, то такой определитель равен нулю.

3. Общий множитель всех элементов какой-либо строки (столбца) можно выносить за знак определителя.

4. Если в определителе поменять поменять местами какие-либо две строки (столбца), то определитель меняет знак.

5. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.

6. Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца) этого же определителя, умноженные на одно и то же число, то определитель не изменится.

7. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором – вторые слагаемые.

Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером.

Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице.

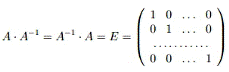
Вырожденной матрицей называется такая матрица, определитель которой равен нулю.

Теорема:

Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.

Дата добавления: 2015-04-24