Взаимное расположение прямых линий и плоскостей в трехмерном пространстве

Взаимное расположение 2 плоскостей: пусть в некоторой аффинной системе координат плоскости s₁ и s₂ своими уравнениями: s₁: А₁х + В₁у + С₁z + D₁=0 (1) и s₂: А₂х + В₂у + С₂z + D₂=0 (2). выясним взаимное расположение этих плоскостей.

Т.к. координаты каждой общей точки плоскостей s₁ и s₂ являются решением системы уравнений (1), (2) и обратно (т.е. каждое решение системы уравнений (1) и (2) является координатами общей точки плоскостей s₁ и s₂), то вопрос о взаимном расположении 2 плоскостей s₁ и s₂ сводится к исследованию системы линейных уравнений (1) и (2).

Обозначим через r и r¢ ранги матриц:

А₁ В₁ С₁ и А₁ В₁ С₁ D₁

А₂ В₂ С₂ А₂ В₂ С₂ D₂

Ясно, что r £ r¢, причем по теореме Кронекера-Капелли система уравнений (1) и (2) совместна Û r = r¢.

Т.о., плоскости s₁ и s₂ имеют хотя бы 1 общую точку Û r = r¢. Возможны следующие случаи:

1) r¢=1. Это означает, что коэффициенты А₁, В₁, С₁ и D₁ уравнения (1) пропорциональны коэффициентам А₂, В₂, С₂ и D₂ уравнения (2) (поэтому r=1) и уравнения (1) и (2) равносильны. отсюда заключаем, что каждая точка одной из плоскостей s₁ и s₂ принадлежит другой плоскости, и поэтому плоскости s₁ и s₂ совпадают. 2 уравнения определяют одну и ту же плоскость.

2) r¢=2, r=2. Тогда плоскости s₁ и s₂ различны (они не могут совпасть, т.к. r¢>1) и имеют хотя бы одну точку, поэтому они пересекаются по прямой.

3) r¢=2, r=1. Система уравнений (1) и (2) несовместна, поэтому плоскости s₁ и s₂ не имеют общих точек, т.е. параллельны.

Взаимное расположение 2 прямых: пусть в пространстве даны: прямая d₁ – точкой М₁ и направляющим вектором`р<sub>1</sub> и прямая d<sub>2</sub> – точкой М<sub>2</sub> и направляющим вектором`р₂.

Прямые d₁, d₂ лежат в одной плоскости Û векторы`М<sub>1</sub>М<sub>2</sub>, р<sub>1</sub>, р<sub>2</sub> компланарны, а значит имеет место равенство:`М₁М₂[ р₁р₂]=0 (1). По векторам`М₁М₂, р₁, р₂ можно определить взаимное расположение данных прямых:

1) прямые скрещиваются. 2 прямые называются скрещивающимися, если они лежат в одной плоскости. Значит, для того, чтобы данные прямые d₁, d₂ были скрещивающимися, необходимо и достаточно, чтобы для них имело место неравенство`М<sub>1</sub>М<sub>2</sub>[`р₁ `р₂]¹0.

2) пусть прямые d₁, d₂ лежат в одной плоскости Þ для них выполняется условие (1). Эти прямые пересекаются Û их направляющие векторы не коллинеарны.

3) прямые d₁, d₂, лежащие в одной плоскости, параллельны, если они имеют общих точек. Это будет только в том случае, когда векторы`р<sub>1</sub>,`р₂ коллинеарны, а векторы `М<sub>1</sub>М<sub>2</sub> и `р₁ не коллинеарны.

4) прямые d₁, d₂ совпадают Û `р<sub>1</sub>,`р₂ и `М₁М₂ попарно коллинеарны.

Взаимное расположение прямой и плоскости: пусть в пространстве дана прямая d точкой М₀(x₀, y₀, z₀) и направляющим вектором `р(`р₁,`р<sub>2</sub>,`р₃), а плоскость s - общим уравнением Ах + Ву + Сz + D=0 в аффинной системе координат. возможны следующие случаи расположения:

1) прямая и плоскость пересекаются, т.е. имеют 1 общую точку. Прямая d пересекает плоскость s Û направляющий вектор р прямой d не параллелен плоскости s, т.е. когда Ар₁ + Вр₂ + Ср₃¹0. Чтобы найти координаты точки пересечения прямой и плоскости, надо решить систему, состоящую из уравнений прямой и плоскости.

2) d||s Û`p||s и т.М₀ не лежит в этой плоскости. Соотношения:

Ар₁ + Вр₂ + Ср₃=0

Аx₀ + Вy₀ + Сz₀ + D ¹0

выражают необходимое и достаточное условия того, что d||s. 3) dÌs Û выполняются равенства:

Ар₁ + Вр₂ + Ср₃=0

Аx₀ + Вy₀ + Сz₀ + D =0.

2. Группа аффинных преобразований плоскости и ее подгруппы. Признаки классификации.

Преобразование плоскости называется аффинным, если оно любые 3 точки М₁, М₂ и М₃, лежащие на одной прямой, переводит в 3 точки М₁¢, М₂¢ и М₃¢, лежащие на одной прямой, и сохраняет их простое отношение, т.е. (М₁, М₂, М₃) = (М₁¢, М₂¢, М₃).

Т.к. преобразование подобия прямую переводит в прямую и сохраняет простое отношение 3 точек, то любое преобразование подобия является аффинным преобразованием. Поэтому любое движение является аффинным преобразованием.

Аффинное преобразование называется преобразованием 1 рода, если оно меняет ориентацию плоскости, и преобразованием 2 рода, если оно меняет ориентацию плоскости.

Обозначим через А множество всех аффинных преобразований плоскости. Докажем, что если f₁ÎA, f₂ÎA, то f₂f₁ÎA. Действительно, т.к. f₁ и f₂ – преобразования, то f₂f₁ – преобразование. Но каждое из преобразований f₁ и f₂ переводит 3 точки, лежащие на одной прямой, и сохраняет их простое отношение, поэтому преобразование f₂f₁ обладает теми же свойствами, т.е. является аффинным преобразованием. Т.о., f₂f₁ÎA.

Если fÎA, то f^-1ÎA. Действительно, если точки А, В и С лежат на одной прямой, то их образы А¢= f^-1(A), В¢= f^-1(В), С¢= f^-1(С) также лежат на одной прямой, ибо если предположить обратное, то найдется такой репер (А¢, В¢, С¢), который в преобразовании f переходит в 3 точки А, В, С, лежащие на одной прямой, что невозможно. При этом, очевидно, преобразование f^-1 сохраняет простое отношение 3 точек.

Т.о., множество А всех аффинных преобразований образует группу. Она называется группой аффинных преобразований плоскости. Основным инвариантом этой группы является простое отношение 3 точек.

Примеры подгрупп:

1) группа Р подобий плоскости;

2) группа D всех движений;

3) множество А₁ всех аффинных преобразований 1 рода;

4) множество А(М₀) всех аффинных преобразований, для которых М₀ – неподвижная точка (группа центро-аффинных преобразований);

5) множество А(а) всех аффинных преобразований, для которых а состоит из неподвижных точек.

Задача на применение движений: даны прямая а и 2 точки А и В, лежащие по одну сторону от этой прямой. Доказать, что на прямой существует единственная точка М₀ такая, что для любой другой точки М этой прямой выполняется неравенство: АМ₀ + ВМ₀ < АМ +ВМ (1).

Решение: Рассмотрим симметрию s относительно прямой а.

Пусть В₁ = s(B). Для произвольной точки М прямой а выполняется равенство ВМ=В₁М₁, поэтому АМ+ВМ=АМ+В₁М.

Пусть М₀ – точка пересечения отрезка АВ₁ с прямой а, а М – произвольная точка прямой а, отличная от т.М₀ (рис.)

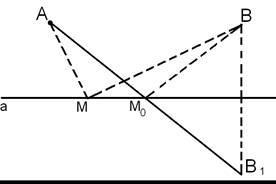
Т.к. т.М₀ лежит между точками А и В₁, то АМ₀+М₀В₁=АВ₁.

С другой стороны, т. А, В₁ и М не лежат на одной прямой, поэтому АВ₁<АМ + МВ₁. Т.о., АМ₀ + М₀В₁<AM + MB₁ или АМ₀ + ВМ₀<АМ + ВМ. Итак, на прямой а существует единственная т.М₀ такая, что для любой другой т.М этой прямой выполняется неравенство.

Задача на применение аффинных преобразований к решению задач: Доказать, что для произвольной трапеции АВСD т.S пересечения прямых, содержащих боковые стороны, середины Е и F оснований АВ и СD, и т.М пересечения диагоналей лежат на одной прямой (рис.).

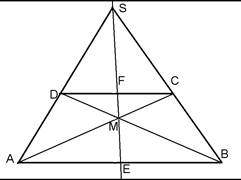
Решение: рассмотрим косое сжатие f с осью ЕS (если прямые, соединяющие соответственные точки перспективно-аффинного преобразования, не параллельны оси, то преобразование называется косым сжатием плоскости.

Нетождественное аффинное преобразование называется перспективно-аффинным, если оно имеет по крайней мере 2 неподвижные точки), при котором т.А переходит в т.В. Т.к. т.Е – середина отрезка АВ, то f – косая симметрия с осью ЕS (т.е. коэффициент k сжатия = -1).

Очевидно, прямая AS переходит в пр.BS, поэтому С = f(D). Но f – косая симметрия, поэтому середина F отрезка DC лежит на оси ES. Т.к. С = f(D), то D = f(C), поэтому пр.АС переходит в пр.ВD и, Þ, т.М пересечения прямых АС и ВD лежит на оси косой симметрии.

Итак, 4 точки Е, S, F и М лежат на одной прямой.

Получаем 4 типа аффинных преобразований:

1) аффинные преобразования, имеющие 2 и только 2 собственных направления,

2) аффинные преобразования, имеющие единственное собственное направление,

3) аффинные преобразования, для которых любое направление является собственным,

4) аффинные преобразования, не имеющие ни одного собственного направления.

Внутри каждого типа можно провести дополнительную классификацию в зависимости от числа неподвижных точек и инвариантных прямых:

1) аффинные преобразования, не имеющие неподвижных точек,

2) центро-аффинные преобразования, т.е. аффинные преобразования, имеющие 1 точку,

3) перспективно-аффинные преобразования, т.е. аффинные преобразования, имеющие неподвижную прямую,

4) тождественное преобразование.

(продолжение вопроса2). Группа аффинных преобразований пространства. Подгруппа движений, признаки классификации. Взаимосвязь движений и подобий.

Преобразование пространства, сохраняющее расстояния, называется движением. Движение, не меняющее ориентацию в пространстве, называется движением первого рода, иначе – второго рода.

Классификация движений пространства:

1) движение имеет по крайней мере 3 инвариантные точки, не лежащие на одной прямой.

Возможны 2 случая: тождественное преобразование (движение 1 рода) и симметрия относительно плоскости (2 рода).

2) движение имеет по крайней мере 2 инвариантные точки А и В, но не имеет инвариантных точек, не лежащих на прямой АВ. Это поворот пространства вокруг прямой АВ на угол j (движение 1 рода).

3) движение имеет только 1 неподвижную точку. Это поворотное отражение (движение 2 рода).

4) движение не имеет ни одной неподвижной точки. Возможны 3 случая: параллельный перенос (движение 1 рода), скользящее отражение (2 рода) и винтовое движение (1 рода).

Преобразование пространства называется преобразованием подобия, если существует такое число k>0, что для любых 2 точек А и В и их образов А¢ и В¢ выполняется равенство: А¢В¢ = kAB.

Любое преобразование подобия пространства с коэффициентом k является произведением гомотетии с тем же коэффициентом k и произвольным центром на некоторое движение.

Преобразование пространства называется аффинным, если оно любые 3 точки М₁, М₂ и М₃, лежащие на одной прямой, переводит в 3 точки М₁¢, М₂¢ и М₃¢, лежащие на одной прямой, и сохраняет их простое отношение, т.е. (М₁, М₂, М₃) = (М₁¢, М₂¢, М₃). Любое преобразование подобия, в частности любое движение, является аффинным преобразованием.

Обозначим через А₃ множество всех аффинных преобразований пространства. Докажем, что если f₁ÎA₃, f₂ÎA₃, то, очевидно, f₂f₁ÎA₃. Действительно, т.к. f₁ и f₂ – преобразования, то f₂f₁ – преобразование. Но каждое из преобразований f₁ и f₂ переводит 3 точки, лежащие на одной прямой, и сохраняет их простое отношение, поэтому преобразование f₂f₁ обладает теми же свойствами, т.е. является аффинным преобразованием. Т.о., f₂f₁ÎA.

Если fÎA, то f^-1ÎA. Действительно, если точки А, В и С лежат на одной прямой, и (АВ, С)=l. Рассмотрим образы точек А и В: А¢= f^-1(A), В¢= f^-1(В). На прямой А¢В¢ возьмем т.С так, чтобы (А¢В¢, С¢)=l, и докажем, что С¢= f^-1(С).,Т.к. f – аффинное преобразование, то (f(А¢)f(В¢), f(С¢))=l или (А¢В¢, f(С¢))=l. Т.о. (АВ, С)=(А¢В¢, f(С¢)), т.е. С¢= f^-1(С).

Т.о., множество А₃ всех аффинных преобразований пространства образует группу. Она называется группой аффинных преобразований пространства.

Подгруппы:

1) Р₃ – группа преобразований подобия пространства.

2) D₃ – группа движений пространства.

3) множество всех аффинных преобразований 1 рода.

4) множество всех аффинных преобразований пространства, каждое из которых оставляет фиксированную т.О неподвижной (группа центро-аффинных преобразований).

5) множество всех аффинных преобразований пространства, для каждого из которых определитель d матрицы =1 (группа эквиаффинных преобразований пространства).

6) группа переносов пространства.

3. Топологические пространства и многообразия. Классификация многообразий. Гомеоморфизм и теорема Эйлера.

Пусть в множестве Х каким-либо способом выделена система Á подмножеств, обладающая свойствами:

1) пустое множество и само множество Х Îсистеме Á.

2) È " семейства подмножеств из системы Á Î системе Á.

3) Ç"конечного семейства подмножеств из системы ÁÎ системе Á.

В этом случае говорят, что на множестве Х определена топологическая структура, а пару (Х, Á) называют топологическим пространством.

Элементы множества Х – точки, элементы из Á - открытые множества пространства (Х, Á).

Примеры:

1) (Е, r),

2) Rⁿ – естественная топология.

3) аффинная плоскость является топологическим пространством.

Пусть (Х, Á) и (Y, T) – топологические пространства. Отображение f: X®Y называется непрерывным в т.хÎХ, если для любой окрестности V точки f(x) в пространстве Y найдется окрестность U т.х в пространстве Х, такая, что f(U)ÌV.

Отображение называется непрерывным, если оно непрерывно в каждой т.х из Х.

Отображение f: X®Y называется гомеоморфизмом, если оно взаимно однозначно и взаимно непрерывно.

Пусть (Х, Á) – топологическое пространство.

k-мерной координатной системой в этом пространстве называется гомеоморфизм j некоторого открытого множества UÌX на открытое множество числового пространства R^k.

Пара (U, j) – k-мерная карта, множество U – координатная окрестность этой карты. k-мерным топологическим многообразием называют отделимое топологическое пространство (Х, Á) со счетной базой, если это пространство можно покрыть координатными окрестностями k-мерных карт (топологическое пространство называется отделимым, если у любых его различных точек $ непересекающиеся окрестности).

Аффинное пространство А_k и евклидово пространство Е_k – k-мерные многообразия.

Пространство (Х, Á) называется k-мерные многообразием с краем, если оно отделимо, имеет счетную базу и его точки можно разбить на 2 непустых класса так, что каждая из точек 1 класса имеет окрестность, гомеоморфную пространству R^k, а каждая из точек другого класса имеет окрестность, гомеоморфную R^k₊, но не имеет окрестности, гомеоморфной R^k.

Любое многообразие с краем, гомеоморфное выпуклому многоугольнику, называется клеткой. образ вершины многоугольника – вершина клетки, образ стороны – сторона клетки.

Пусть К – клеточное разложение двумерного многообразия F. Точка хÎF называется вершиной клеточного разложения К, если х – вершина хотя бы 1 клетки из К.

Фигура gÌF называется стороной разложения К, если она является стороной хотя бы 1 клетки К.

Введем обозначения: a₀ – число вершин, a₁ – число сторон, a₂ – число клеток разложения К.

Число c(F) = a₀ – a₁ + a₂ называется эйлеровой характеристикой многообразия F.

Теорема Эйлера: В любом простом многограннике сумма числа вершин и числа граней на 2 единицы больше числа его ребер. Док-во: рассмотрим произвольный простой многогранник F и обозначим через a₀, a₁, a₂ число вершин, ребер, граней.

Грани многогранника F образуют клеточное разложение его границы b(F), и поэтому эйлерова характеристика c(b(F)) границы b(F) равна a₀ – a₁ + a₂. Но по определению простого многогранника c(b(F)) =2. Т.о. a₀ – a₁ + a₂ = 2, или a₀ + a₂ =a₁ + 2. читд

Если в некотором клеточном разложении К многообразия F клетки можно ориентировать так, что каждые 2 клетки, имеющие общую сторону, будут одинаково ориентированы, то многообразие F называется ориентируемым.

Если же такого клеточного разложения не существует, то многообразие F называется неориентируемым.

Граница любого тетраэдра ориентируема. Лист Мебиуса – пример неориентируемого компактного многообразия с краем.

Дата добавления: 2015-04-24