Векторы в трехмерном пространстве. Операции над векторами. Векторный подход к решению задачи.

Отрезки АВ и СD называются эквиполлентными, если они одинаково направлены и имеют равные длины.

Вектор – множество всех направленных отрезков, любые 2 из которых эквиполлентны.

Операции над векторами:

1. возьмем произвольные векторы`а и`b. От какой-нибудь т.А отложим вектор АВ =`а, затем от т.В отложим вектор ВС=`b. Вектор АС=`с называется суммой векторов `а и`b и обозначается так: с = а + b.

Для нахождения суммы 2 неколлинеарных векторов используют правило треугольника и параллелограмма.

Для произвольных векторов а, b, с справедливы следующие равенства: 1) а + b = b + а. 2) (а + b) + c = a + (b + c).

Для построения суммы нескольких векторов используется правило многоугольника.

2. Разностью векторов а и b называется такой вектор х, что b + x = a.

3. Произведением вектора а на число a называется вектор р, который удовлетворяет условиям:

1) |p|=|a||a|, где |a| - абсолютное значение числа a;

2) р­­а, если a³0 и р­¯а, если a<0.

Для произвольных чисел a, b и векторов а и b справедливы след.равенства:

1) 1×а=а и -1×а = -а.

2) a(bа) = (ab)а.

3) a(а + b)=aа + ab.

4) (a + b)а=aа + bа.

4. Скалярным произведением 2 векторов называется число, равное произведению их длин на косинус угла между ними.

Для произвольного числа a и произвольных векторов а, b, с справедливы след.равенства:

1) ab = ba,

2) (aa)b = a(ab) и a(ab) = a(ab).

3) (a + b)c = ac + ab.

5. Смешанным произведением некомпланарных векторов а, b, с, взятых в данном порядке, называется объем параллелепипеда, построенного на этих векторах, снабженный знаком «-», если базис а, b, с правый, и знаком «+», если этот базис левый.

Для произвольных векторов а, b, с, d и произвольного числа a имеют место след.равенства:

1) abc = bca = cab,

2) abc = -bac, abc = -cba, abc = -acb.

3) (aa)bc = a(abc), a(ab)c=a(abc), ab(ac)=a(abc).

4) (a+b)cd=acd+bcd, a(b+c)d=abd+acd, ab(c+d)= abc+abd.

6. Векторным произведением неколлинеарных векторов а и b, взятых в данном порядке, называется вектор р, длина которого численно равна площади параллелограмма, построенного на этих векторах; этот вектор ^векторам а и b и направлен так, что базис a, b, p имеет правую ориентацию.

Для произвольных векторов a, b, c и произвольного числа a имеют место след.равенства:

1) [ab]=-[ba],

2) [aa,b]=a[ab], [a,(ab)]=a[ab],

3) [a+b,c]=[ac]+[bc], [a,b+c]=[ab]+[ac].

Рассмотрим систему векторов а₁, а₂, …, а_n и зададим n действительных чисел a₁, a₂, …, a_n.

Вектор b=a₁а₁ + …+ a_nа_n называется линейной комбинацией данных векторов.

Система векторов называется линейно зависимой, если $числа a₁, a₂, …, a_n, среди которых хотя бы 1 отлично от 0, и такие, что a₁а₁ + …+ a_nа_n = 0.

Базисом векторного пространства называется такая система векторов, которая задана в определенном порядке и удовлетворяет условиям:

1) система линейно независима.

2) "вектор пространства является линейной комбинацией данной системы векторов.

Пусть е₁, е₂, е₃ – данный базис, а – произвольный вектор пространства. $единственные числа а₁, а₂, а₃ такие, что: а=а₁е₁ + а₂е₂+а₃е₃. Говорят, что вектор а разложен по векторам базиса. Коэффициенты а₁, а₂, а₃ называются координатами вектора а в этом базисе.

Базис i, j, k называется ортонормированным, если его векторы удовлетворяют 2 условиям:

1) |i| = |j| = |k| = 1.

2) если ОЕ₁ = i, OE₂ = j, OE₃ = k, то углы Е₁ОЕ₂, Е₁ОЕ₃ и Е₂ОЕ₃ прямые.

Длина вектора а(а₁, а₂, а₃) в ортонормированном базисе вычисляется по формуле: |a| = .

6. Общая теория линий 2 порядка. Классификация линий. Теорема о подобии линий 2 порядка.

В аффинной системе координат Ое₁е₂ общее уравнение линий 2 порядка имеет вид: а₁₁х² + 2а₁₂ху + а₂₂у² + 2а₁₀х + 2а₂₀у + а₀₀ = 0. Коэф. этого уравнений – любые действительные числа, причем а₁₁, а₁₂, а₂₂ не равны одновременно 0.

Для того, чтобы привести это уравнение к каноническому виду, необходимо:

1) найти корни характеристического уравнения: l² – (а₁₁+а₂₂)l + (а₁₁а₂₂ – а₁₂²) = 0.

2) найти координаты векторов i¢(cosa, sina) и j¢(-sina, cosa) по формулам.

3) вычислить коэф. а¢₁₀, а¢₂₀ по формулам: а¢₁₀ = а₁₀cosa + a₂₀sina, a¢₂₀ = - a₁₀sina + a₂₀cosa, a¢₀₀ = a₀₀. И записать уравнение линии g в виде: l₁х¢² + l₂у¢² + 2а¢₁₀х¢ + 2а¢₂₀у¢ + а₀₀ = 0.

4) Переносом начала координат получить каноническое уравнение линии g.

5) построить систему координат О¢i¢j¢ по координатам т.О¢ и векторов i¢ и j¢ и затем построить точки линии g в системе О¢i¢j¢ по каноническому уравнению.

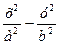Примеры: 1) Эллипс: =1. 2) Гипербола: =1. 3) Парабола: у²=2рх.

Эксцентриситетом называется число e = c/a, где с – фокальное расстояние, а а- большая полуось.

Теорема: 2 эллипса, эксцентриситеты которых равны, подобны.

Док-во: пусть в ортонормированных реперах (О, Е₁, Е₂) и (О¢, Е¢₁, Е¢₂) данные эллипсы g и g¢, эксцентриситеты равны, имеют соответственно канонические уравнения: =1 и 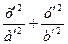=1. Докажем, что g~g¢. Рассмотрим движение f₁, которое репер (О, Е₁, Е₂) переводит в (О¢, Е¢₁, Е¢₂).

При этом движении эллипс g переходит в некоторый эллипс g₁, который в репере имеет уравнение =1.

Эллипсы g и g¢ имеют равные эксцентриситеты e. b/a = 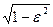, b¢/a¢ = 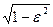, поэтому a/a¢ = b/b¢.

Гомотетия f₂ c центром О¢ и коэф. а¢/а в репере (О¢, Е¢₁, Е¢₂) задается формулами: х¢=а¢х/а, у¢=b¢у/b или х = ах¢/а¢, e = be¢/b¢.

Образом эллипса g₁ приэтой гомотетии является линия 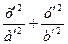=1, т.е. эллипс g¢. Т.к. f₁ и f₂ являются преобразованиями подобия, то f₂f₁ – подобие, которое переводит g в g¢, поэтому g~g¢.

Теорема: 2 гиперболы, эксцентриситеты которых равны, подобны.

Теорема: любые 2 параболы подобны.

(это не надо, почитайте так для интереса).8. Построения на плоскости с помощью циркуля и линейки без делений. Методы построений.

Следующие шаги построения мы считаем выполнимыми:

1) построение прямой, проходящей через 2 построенные точки.

2) построение окружности с центром в построенной точке и с радиусом, равным отрезку с концами в построенных точках.

3) построение точки пересечения 2 непараллельных построенных прямых.

4) построение точек пересечения построенной окружности и построенной прямой, если они пересекаются.

5) построение точек пересечения 2 построенных окружностей, если они пересекаются.

Основные построения:

1) Отложить на данном луче от его начала отрезок, равный данному отрезку.

2) отложить от данного луча в данную полуплоскость угол, равный данному углу.

3) построить треугольник по 3 сторонам.

4) построить треугольник по 2 сторонам и углу между ними.

5) построить треугольник стороне и 2 прилежащим углам.

6) построить биссектрису данного неразвернутого угла.

7) построить серединный ^ данного отрезка.

8) построить середину данного отрезка.

9) построить пр., проходящую через данную точку и перпендикулярную данной прямой.

10) построить пр., проходящую через данную точку и параллельную данной пр.

11) построить прямоугольный треугольник по гипотенузе и острому углу.

12) построить прямоугольный треугольник по гипотенузе и катету.

13) построить касательную к окружности, проходящую через данную на ней точку.

Схема решения задач:

1) Анализ - или поиск решения задачи состоит в установлении зависимостей между данными фигурами и искомой фигурой с целью нахождения способа решения задачи.

2) Построение – состоит в последовательном перечислении тех построений, которые надо выполнить для решения задачи.

3) доказательство – состоит в том, чтобы установить, что построенная фигура действительно удовлетворяет всем условиям, поставленным в задаче.

4) исследование – состоит в том, чтобы ответить на вопросы: 1. при всяком ли выборе данных задача имеет решение.

2. сколько различных решений имеет задача при каждом возможном выборе данных.

Методы:

1) метод пересечений – задачу сводят к построению одной т.Х, которая удовлетворяет 2 условиям, вытекающим из постановки задачи.

Пример: построить окружность, касательную к двум данным параллельным пр. а и b и проходящую через данную т.М.

Решение:

1) Анализ: предположим, что задача решена и w - искомая окружность с центром О. Если мы построим т.О, то окружность (О, ОМ) будет искомой.

Т.о., задача сводится к построению т.О. т.О удовлетворяет след. 2 условиям: 1. эта точка равноудалена от параллельных пр. а и b. 2. отстоит от точки М на расстоянии d/2, где d – расстояние между параллельными пр. а и b.

Множество точек F₁, равноудаленных от пр. а и b, есть пр., а множество точек F₂ – есть окружность (М, d/2).

2) Построение: 1. строим какой-нибудь общий ^ АВ данных параллельных пр.а и b. 2. строим серединный ^m отрезка АВ. Пусть т.С – т.пересечения АВ и m. 3. строим окружность (М, АС). Обозначим через О т.пересечения пр.m и окружности (М, АС). 4. строим искомую окружность.

3) Доказательство: окружность (О, ОМ) по построению проходит через т.М. Она касается пр.а и b, т.к. ОМ=АС=АВ/2=d/2.

4) Исследование: ясно, что задача имеет решения Û пр.m и окружность (М, АС) имеют общие точки, причем число решений равно числу общих точек пр.m и окружности (М, АС).

Возможны 3 случая: 1. т.М лежит между 2 паралл.пр. а и b. Тогда r(m, M)<AC, поэтому окружность (М, АС) и пр.m имеют 2 общие точки. В этом случае задача имеет 2 решения. 2. т.М лежит на одной из пр. а или b.

В этом случае r(m, M)=АС, поэтому окружность (М, АС) касается пр.m, т.е. задача имеет только 1 решение. 3. т.М лежит вне полосы, ограниченной прямыми а и b. В этом случае r(m, M)>АС, поэтому окружность (М, АС) и пр.m не имеют общих точек. задача не имеет решений.

2) метод преобразований – наиболее часто применяются преобразования подобия, особенно гомотетии, различные виды движений, а также инверсия.

Пример (метод паралл.переноса): построить трапецию по заданным ее сторонам.

Решение:

1) Анализ: допустим, что задача решена и АВСD – искомая трапеция. Рассмотрим вспомогательную фигуру – треугольник АВD¢, сторона ВD¢ которого является образом отрезка CD при паралл.переносе на вектор СВ. Треугольник АВD¢ легко построить по 3 сторонам АВ =с, ВD¢=CD=d, AD¢=AD-BC=a-b. Построив треугольник АВD¢, легко построить искомую трапецию АВСD.

2) Построение: 1. проведем произв.пр. р и от некоторой т.D этой пр.на одном из лучей отложим отрезки DA=a, DD¢=b.

2. строим треуг. АВD¢ так, чтобы АВ=с, BD¢=d.

3. Строим параллелограмм DD¢BC по 3 вершинам D, D¢, B. Вершина С является т.пересечения окружностей (В, b) и (D, d). АВСD – искомая трапеция.

3) Исследование: задача имеет решение Û $D АВD¢, стороны которого соответственно равны а¢, с и d, где а¢=a-b, т.е. когда a>b и наибольшее из чисел а¢, с и d меньше суммы 2 других.

3) Алгебраический метод: задачу формулируют так, чтобы в качестве данных фигур и искомой фигуры были отрезки. Используя подходящие теоремы, выражают длину искомого отрезка через длины данных отрезков и по найденной формуле строят искомый отрезок.

Пример: Вписать в данную окружность (О, r) правильный десятиугольник.

Решение: пусть АВ – сторона прав.10-уг., вписанного в окружность (О, r), а х – длина отрезка АВ. Проведем бисс-су ВМ угла В DОАВ. Т.к. DОАВ – равнобедренный и ÐО=36⁰, то ÐВ=72⁰, ÐА=72⁰, поэтому ÐАВМ=36⁰.

Т.о., DАВМ~DАОВ, поэтому АВ/AM=AO/AB, откуда х/(r-x)=r/x, или х²+xr-r²=0. Это уравнение имеет след.корни: х₁ = -r/2 + , х₂ = -r/2 - . Т.к. х₁>0, x₂<0, то х соответствует х₁, который и является стороной прав.10-уг.

Дата добавления: 2015-04-24