Биноминальное распределение

Теорема Пуассона

Формула Бернулли

Вероятность того, что в серии из n испытаний (независимых) событие A появится ровно k раз и не появится n-k раз равна:

P_n(k)=C^k_n*p^k*q^n-k

Пример

p=0,9 q=0,1; n=4; k=3

P₄(3)=C³₄*0,9³*0,1=0,2916

Формула Бернулли применима к небольшим числам.

Если вероятность P наступления события A в каждом испытании постоянна и мала, а число независимых испытаний n достаточно велико, то вероятность того, что событие A наступит ровно k раз приближенно равна:

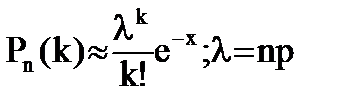
При npq≥10, то применяют формулы Лапласса, если npq<10, то формулы Пуассона.

Пример

Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что при транспортировке будет повреждено не более 3х изделий?

О. Закон распределения дискретной случайной величины, определяемой формулой Бернулли, называется биноминальным.

X: число появлений события А в n независимых испытаниях. Событие А появляется с вероятностью p в одном испытании и не появляется с вероятностью q.

Табличный вид биноминального распределения

X				….	k	n
P	q^n	Cn^1*p^1*q^n-1	Cn^2*p^2*q^n-2		Cn^k*p^k*q^n-k	p^n

X: число появления события A в 1 испытании.

Y
P	q	p

M(Y)=0*q+1*p=p

X=Y₁+Y₂+…+Y_n

M(X)=M(Y₁)+M(Y₂)+…+M(Y_n)=np - математическое ожидание биноминального распределения

Дисперсия дискретной случайной величины находится по формуле:

D(X)=M(X²)-(M(X))²

Найдем по формуле дисперсию случайной величины Y:

M(Y²)=0²*q+1²*p

D(Y)=p-p²=p(1-p)=pq

D(X)=D(Y₁)+D(Y₂)+…+D(Y_n)=npq

D(X)=npq – Дисперсия биноминального распределения

Среднее квадратическое отклонение биноминального распределения -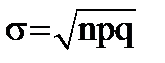

qⁿ+ C_n¹*p¹*q^n-1+C_n¹*p¹*q^n-1+…+C_n^k*p^k*q^n-k+pⁿ=(q+p)ⁿ=1

Дата добавления: 2015-04-24