Вопрос № 24. Определение операции умножения матриц. Примеры. Свойства умножения. Перестановочные матрицы. Примеры

Этих операций.

Вопрос № 23. Линейные (сложение и умножение на число) операции с матрицами Свойства

⊐ А и В – матрицы одинаковой размерности. Их суммой будет матрица той же размерности, эл-ты к-ой равны суммам эл-ов, стоящ.на соотв.местах

Аm+n Bm+n

Cm+n= (Аm+n+ Bm+n) ⟷ (Cij=aij+bij)

A+B = + =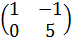

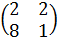
Св-ва сложений:

1) А+В = В+А

2) (А+В)+С=А+(В+С)

3) Существование нуля

⊐ 0: А+0=А

0 – нулевая матрица той же размерности, что и А. Матрица наз.нулевой, если все её эл-ты равны 0

Оm*n =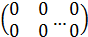

4) Существование противоположной матрицы

∃В: А+В = 0

В= 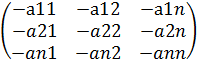= - A

Умножение числа на матрицу

k∊R (k∊C)

Произведением числа на матрицу будет матрица той же размерности, все элементы к-ой равны произв.k на соотв.эл-ты исходной матрицы.

(В=kA)⟷(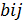 = k∙aij; i=1…m; j=1…n)

2∙ =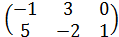

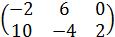
i ∙ =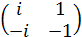

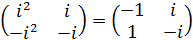
Св-ва умножения:

1) kA=Ak

2) k(lA) = (kl)A = l(kA)

3) k(A+B) = kA+kB

4) (k+l)A = kA + lA

3∙

Умножение 2-х матриц: умножение А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произведением матрицы А размера mxk на матрицу В размера kxn называется матрица С размера mxn, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы

Пр.: А∙В =

С11=1*0+2*1+(-3)*(-2)= 8

С12= 1*6+2*(-1)+(-3)*4= -8

С21=0*0+4*1+7*(-2)= -10

С22= 0*6+ 4*(-1)+7*4= 24

Св-ва умножения матриц:

1) АВ≠ВА

2) А(ВС)=(АВ)С

3) А(В+С)=АВ+АС

В тех случаях, когда АВ=ВА, то говорят, что матрицы А и В перестановочные (они коммутируют).

Пр.: АВ =

ВА =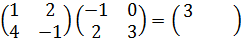

-1≠3⇒ АВ≠ВА

№25
Системы двух линейных ур-ий с двумя неизв. Имеют вид:
ax+by=c
dx=ey=f
где a,b,c,d,e,f-заданные числа,x,y-неизвестные.Числа
a,a,d,e-коэффициенты при неизвестных;с,f-свободые члены.Решение этой
системы может быть найдено двумя основными методами(подстановка,сложение
/вычетание)

Определители второго порядка,соотв. Данной матрице,наз.число,обознач.
символом
|a11 a12|
detA= | |
|a21 a22|

и определяемое рав-вом detA=a11a22-a12a21

Диагональ,образ. эл-тами a11 и a12,наз. главной
Диагональ,образ. эл-тами a12 a21,наз. Побочной

Теорема. (Правило Крамера)

Теорема. Система из n уравнений с n неизвестными

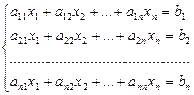
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = D_i/D, где

D = det A, а D_i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

D_i =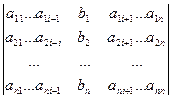

Пример.

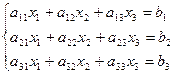
A = 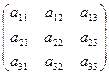; D₁= ; D₂= ; D₃= ;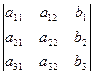

x₁ = D₁/detA; x₂ = D₂/detA; x₃ = D₃/detA;

№26
Определители третьего порядка наз. число квадратной матрицы третьего
порядка,обозн. cимволом
|a11 a 12 a 13 |
A= |a21 a 22 a23 |
|a31 a32 a 33|
и определяемое рав-вом
detA=a11a22a33+a12a23a31+a13a21a32-a31a22a13-a21a12a33-a11a32a23
Диагональ,образ. эл-тами а11,а22,а33,наз. главной
Диагональ,образ. эл-тами а31,а22 и а13,наз. Побочной

Теорема (разложение определителя по строке или столбцу).

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки

d = a_{i 1} A_{i 1} + a_{i 2} A_{i 2} +... + a_{i n} A_{i n} (i = )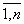

или j- го столбца

d = a_{1 j} A_{1 j} + a_{2 j} A_{2 j} +... + a_{n j} A_{n j} (j = ).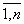

В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

Билет №27. Перестановки чисел 1,2,3,..., n. Инверсии. Подсчёт числа инверсий и четность-нечетность перестановки. Определители произвольного порядка.

Перестановка – упорядоченный набор чисел 1,2..n, трактуемый как биекция на множестве {1,2,…n}, в котором числу 1 ставят в соответствии i-тый элемент из набора N – порядок перестановки.

Перестановка является четной, если число инверсий четно. Нечетной, если число инверсий нечетно.

Инверсией в перестановке π порядка n называется всякая пара индексов i, j такая, что 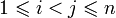и π(i) > π(j). Чётность числа инверсий в перестановке определяет чётность перестановки.

Дата добавления: 2015-04-24