Билет №29. Матричная запись системы линейных уравнений. Решение систем n линейных уравнений с n неизвестными при помощи обратной матрицы

Билет №28. Обратная матрица(определение, единственность).Необходимое и достаточное условие её существования (с доказательством).

Матрица B называется обратной матрицей для квадратной матрицы A, если АВ=ВА=Е (Обратная матрицы для матрицы А обозначается A^-1 .) Если определитель матрицы равен нулю, то обратная к ней не существует. Если обратная матрица существует, то она единственна.)

Обратная матрица существует тогда и только тогда, когда определитель матрицы А не равен нулю.

(A^-1 ) ↔ (detA≠0)

Det(AB)=detA∙detB

detE=det(A∙ A^-1 )=det A^-1 ∙detA=1 → detA≠0

Системой m линейных уравнений с n неизвестными называется системой вида.

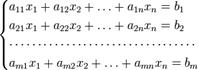
Где аij коэффициент при xj

Х1, х2…хn – неизвестные

B1, b2…bm – свободные члены

можно представить в матричном виде

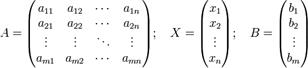
Х – вектор неизвестных, В – вектор свободных членов

и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{- 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{- 1} AX = A ^{- 1} B

A ^{− 1} A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{- 1} B.

Билет №30. Теорема Крамера для систем n линейных уравнений с n неизвестными (доказательство для п =3).

Если определитель отличен от нуля, следовательно, можно применить правило Крамера:

Если определитель матрицы не равен нулю, то система имеет решение и притом единственное. Это решение задается формулой:

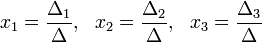
Дата добавления: 2015-04-24