Определение геометрической вероятности

Вопрос № 35. Геометрическое определение вероятности. Проверка выполнения аксиом. Примеры решения задач с использованием геометрического определения.

Предположим, что пространство элементарных событий имеет мощность континуума. Будем рассматривать такие подмножества, которые являются измеримыми, т.е. имеют меру – функцию множества. Такую, что мера от А всегда неопределенна, мера (А+В)=(А+В), если пересечение множеств А и В пусто.

Ϭ(сигма) алгебра событий – алгебра измеримых множеств.

По определению, вероятность события А – отношение меры А к мере пространственно-элементарных событий.

Геометрическое определение вероятности - Вероятность случайного события равна отношению площади области, благоприятствующей данному событию к площади, соответствующей всевозможным исходам эксперимента

Р(А)=S(A)/S(Ω)

Проверка выполнения аксиом:

А1.
=1(верно)

А2

Отношение площадей неотрицательно и не превышает единицы, так как площадь части области не больше площади всей области.

- эта дробь не может быть отрицательной

А3

Геометрическая вероятность суммы несовместных событий равна сумме их вероятностей. Полный набор событий изображается разбиением области Ω на непересекающиеся области, объединение которых совпадает со всей областью Ω. Поэтому сумма геометрических вероятностей событий образующих полный набор равна 1

Мера
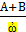= + =р(А)+р(В)

Задача о круге

В круг радиуса R наудачу бросается точка. Найти вероятность того,

что она попадет в фиксированный квадрат,

вписанный в данный круг?

Ω - круг

А – попадание в квадрат

Р(А)= S(A)/S(Ω)=а² /πr² =2/π

Вопрос № 36. Свойства вероятностей (сумма вероятностей противоположных событий, вероятность частного случай, теорема сложения - все с доказательствами)

Сумма событий А и В есть не что иное как обьединение соответсвующих множеств

A+B= A нижн.пересеч.В

По определению сумма событий-это событие,состоящее в том,что произошло событие А или событие В.

Событию А+В соответствует множество элементарных исходов,принадлеж.множеству А или множеству В те именно обьединение этих множеств.

Произведение событий есть пересечение соответствующих множеств

АВ=А∩В.

События несовместны если пересечение соответствующих множеств пусто.

Вероятность противоположного события вместе с вероятностью исходного события равна 1

Р(А)+Р(Ā)=1

Доказательство:

Ω=А+Ā

А*Ā=Ø

Р(А+Ā)=Р(Ω)=1 => 1=Р(А)+Р(Ā)

Если событие А является частным случаем события В, то вероятность А НЕ превосходит вероятность В.

В=А+(В-А)

А*(В-А) – невозможно, эти два события несовместны, но по третьей аксиоме (для любых несовместных событий вероятность суммы событий равна сумме их вероятностей) Р(В)=Р(А+(В-А))=Р(А)+Р(В-А)

В-А=В*Ā

Тогда по второй аксиоме (для любого события А верно, что вероятность А неотрицательна) Р(В-А)≥0 (как и у любого из алгебры событий)

Р(А)<Р(В)

Теорема Сложения.

Р(А+В)=Р(А)+Р(В)-Р(А*В)

P.S.Если А*В=Ø, то Р(А*В)=0, получаем третью аксиому (частный случай)

Доказательство:

А+В=(А-В)+(В-А)+А*В

А и В-А несовместны

А*(В-А)=Ø – невозможное событие

(Р(А+В) = Р(А)+Р(В-А)) – (Р(В)=Р(В-А)+Р(А*В)) = (Р(А)=Р(А)-Р(А*В))

Р(А+В)=Р(А)+Р(В)-Р(А*В)

Дата добавления: 2015-04-24