Индексный метод анализа факторов

Некоторые социально-экономические показатели находятся между собой в определенной (функциональной) связи, например, в виде произведения (либо отношения). В таком же соотношении должны находиться и статистические показатели, характеризующие изменение исходных социально-экономических показателей (т. е. индексы).

Если , то .

Данное соотношение между индексами осуществимо, если веса индексирования для I_X и I_Y берутся за разные периоды времени (или относятся к разным объектам), т. е. один из индексов должен быть построен по формуле Ласпейреса, а другой – по формуле Пааше:

.

Индексный метод позволяет также представить абсолютное изменение результативного показателя () как результат влияния различных факторов (входящих в формулу его расчета).

Общее абсолютное изменение результативного показателя текущего уровня по сравнению с базисным определяется как разница между числителем и знаменателем в формуле сводного индекса данного результативного показателя:

.

Оно может быть разложено на составляющие: абсолютные изменения за счет отдельных факторов, входящих в его расчетную формулу (, ).

51. Взаимосвязь между индексами переменного, постоянного состава и структурных сдвигов.

Индексы позволяют анализировать изменения не только агрегатов, но и их средних величин с помощью индексов переменного и постоянного состава и структурного сдвига. Если индексируемую величину обозначить через X, а веса усреднения – через f, то индекс средней величины можно записать так:

.

Данный индекс называют еще индексом переменного состава (I_пс)

Если при расчете индекса средних величин использовать веса усреднения одного и того же уровня (либо текущего – f₁, либо базисного – f₀), то влияние изменения структурного фактора на изменение средней величины будет устранено. Такой индекс называют индексомфиксированного (постоянного) состава – I_фс:

.

Если при расчете индекса средних величин использовать значения усредняемого признака X одного и того же уровня (либо текущего – Х₁,либо базисного – Х₀),то на изменение средних будет оказывать влияние только изменение весов, т. е. структуры совокупности. Этот индекс условно называют индексом структуры (или индексом структурного сдвига):

.

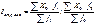Индекс структуры показывает, в какой степени изменение средней величины индексируемого показателя произошло за счет изменения структуры (состава) совокупности.

Между индексами переменного, постоянного состава и структурных сдвигов существует следующая взаимосвязь:

.

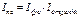52. Классификация связей в статистике

Признаки, которыми характеризуются единицы совокупности, могут быть взаимосвязанными. Взаимосвязанные признаки выступают в одной из ролей:

•роли признака-результата (Y);

•роли признака-фактора, значения которого определяют значение признака-результата (X).

Связи классифицируют по степени тесноты, направлению, форме, числу факторов.

1) По степени тесноты связи делят на статистические и функциональные.

Статистическая (стохастическая) связь – это такая связь между признаками, при которой для каждого значения признака-фактора X признак-результат Y может в определенных пределах принимать любые значения с некоторыми вероятностями; при этом его статистические (массовые) характеристики (например, среднее значение) изменяются по определенному закону.

Y=f(X, и),

где Y – фактическое значение результативного признака;

f(X) – часть результативного признака, сформировавшаяся под воздействием фактора X (или множества факторов: Y=f(X₁,...,X_m);

и – случайная составляющая, часть результативного признака, возникшая вследствие действия прочих (неучтенных) факторов, а также ошибок измерения признаков.

Корреляционная связь – частный случай статистической связи. При корреляционной связи с изменением значения признака X среднее значение признака Y закономерно изменяется, в то время как в каждом отдельном случае признак Y (с различными вероятностями) может принимать множество различных значений.

Функциональная связь – такая связь, когда каждому возможному значению признака-фактора X соответствует одно или несколько строго определенных значений результативного признака Y. Она имеет место, когда все факторы, действующие на результативный признак, известны и учтены в модели и ошибки измерения отсутствуют.

Y=f(X).

2) По направлению связи делятся на прямые и обратные.

При прямой связи направление изменения результативного признака совпадает с направлением изменения признака-фактора.

При обратной связи направление изменения результативного признака противоположно направлению изменения признака-фактора.

3) По форме связи (виду функции f) связи делят на линейные (прямолинейные) и нелинейные (криволинейные) связи.

Линейная связь отображается прямой линией; криволинейная – кривой (параболой, гиперболой и т. п.).

4) По количеству факторов, действующих на результативный признак, связи подразделяют на однофакторные (парные) и многофакторные связи.

Дата добавления: 2015-04-24