Потенциальность электростатического поля. Потенциал поля точечного заряда

Напряжённость поля точечного заряда Q известна в любой точке пространства: .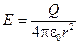

Так как это сферически симметричное поле, его потенциал будет меняться только как функция r. Поэтому связь напряжённости и потенциала можно упростить и записать так: 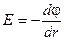. Или: .Разность потенциалов двух точек поля:

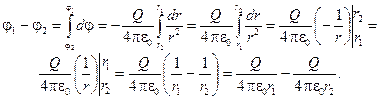
Полученный результат позволяет сделать два вывода:

1. Потенциал произвольной точки поля точечного заряда обратно пропорционален расстоянию от заряда до рассматриваемой точки: .

2. Потенциал бесконечно удалённой точки (r ₂ ® ¥) равен нулю j_¥ = 0.

Множество точек одинакового потенциала образует в пространстве сферические эквипотенциальные поверхности.

5. Работа сил электрического поля по переносу заряда. Разность потенциалов. Теорема о циркуляции электростатического поля. Электрический потенциал. Связь между напряжённостью электростатического поля и потенциалом.

Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика.

Потенциал — энергетическая характеристика поля, связанная и с энергией заряда в электростатическом поле и с работой, совершаемой электрической силой при перемещении заряда.

Вспомним, что силы, работа которых не зависит от вида траектории и определяется только положением её начальной и конечной точек, называются консервативными.

Мы пришли к выводу, что кулоновская сила консервативна. Впрочем, ничего неожиданного в этом выводе нет: ведь сила взаимодействия двух точечных зарядов может быть отнесена к классу центральных сил, а все центральные силы, как было установлено в механике, консервативны.

Итак, вычислим работу кулоновской силы при перемещении заряда q из точки 1 в положение 2 (по любой траектории):

Энергия единичного (q = 1) точечного заряда уже не будет связана с величиной этого пробного заряда q и может быть принята в качестве энергетической характеристики данной точки электростатического поля:

.

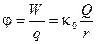Эта энергетическая характеристика поля получила название потенциал — j.

Потенциал произвольной точки электростатического поля равен энергии единичного положительного заряда, помещённого в эту точку.

Потенциал некоторой точки электростатического поля равен работе, совершаемой электрической силой при эвакуации единичного положительного заряда из этой точки в бесконечность:

.

Потенциал поля, созданного системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов в отдельности: . - «принцип суперпозиции для потенциала»

Разность потенциалов двух точек поля равна работе, совершаемой электрической силой при перемещении единичного заряда из первой точки во вторую:

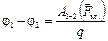
Потенциал и напряжённость — две локальные характеристики электростатического поля. То есть, это две характеристики — энергетическая и силовая — одной и той же точки поля.

Разумно предположить, что между ними должна существовать однозначная связь.

напряжённость электростатического поля равна градиенту потенциала с обратным знаком. 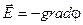. Здесь векторный оператор «градиент»

grad = .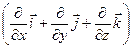

Так как это сферически симметричное поле, его потенциал будет меняться только как функция r. Поэтому связь напряжённости и потенциала можно упростить и записать так: .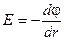

Теорема о циркуляции электростатического поля. Интеграл по замкнутому контуру 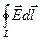= называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.

Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю: .

Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.

Дата добавления: 2015-04-24