Неполноценность I начала термодинамики. Различные формулировки второго начала. Круговые процессы. Тепловые машины

I начало терм-ки не указывает направление протекания процесса, поэтому его недостаточно для описания темодинамич. процессов.

Феноменологич. формулировка II начала терм-ки: вечный двигатель II рода невозможен.

Вечный двигатель II рода - периодически действующий двигатель, совершающий работу только за счёт охлаждения источника тепла.

Его КПД = 1, т.е. это двигатель, работающий только за счёт получения тепла из вне.

Различные формулировки 2 начала терм-ки:

Клаузиус: невозможен самопроизвольный переход тепла от менее нагретого тела к более нагретому телу.

Томсон: не возможен круг

Кельвин: невозможны процессы, единственным результатом которых было бы превращение тепла целиком в работу. Другими словами – невозможен тепловой двигатель второго рода с КПД=1.

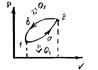
Круговой процесс – это процесс при котором система проходя через ряд состояний возвращается в исходное. Круговые процессы делятся на прямые(проходят по часовой стрелки работа за цикл больше 0;_1а2-А_2б1) и обратные(процесс проходит против часовой, работа за цикл меньше 0) А=А_2в1-А_1а2. В результате кругового процесса система возвращается в исходное состояние и следовательно полное изменение внутренней энергии газа равно 0, поэтому первое начало термодинамики для кругового процесса Q=A. Прямой цикл используется в тепловых двигателях, обратный цикл в холодильных машинах.

80. Адиабатный процесс. Уравнение адиабаты. Политропный процесс.

Адиабатическим наз. процесс при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. dА = -dU, т.е. внешняя работа совершается за счет изменения внутренней энергии системы. Для произвольной массы газа:

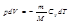продифференцировав уравнение состояния для идеального газа, получим: 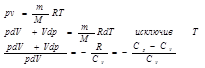разделив переменные и учитывая, что Ср/Сv= g найдем

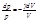интегрируя это выражение в пределах от р1 до р2 и соответственно от V1 до V2, а затем потенцируя получим: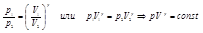

- уравнение адиабатического процесса. (уравнение Пуассона) g- показатель адиабаты

Работа в адиабатическом процессе:

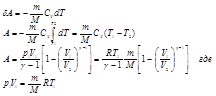
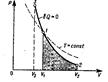Процесс в котором теплоёмкость остаётся постоянной наз. политропным.

cm = const

cm – молярная теплоемкость.

Найдем уравнение политропы для идеального газа. Из первого начала термодинамики следует

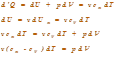
Из уравнения состояния идеального газа следует

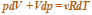
Поэтому можно записать

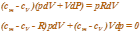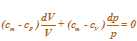Поскольку c_P = c_V + R то

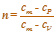
Обозначив получаем

Интегрируем

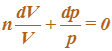Значит уравнение политропы

n - показатель политропы

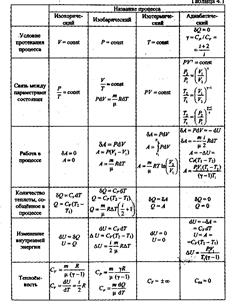
Все предыдущие процессы являются частными случаями политропического процесса:

n = 0 изобара c_m = c_P, n = 1 изотерма c_m = ¥

n = ¥ изохора c_m = c_V n = g изобара c_m = 0.

Дата добавления: 2015-04-24