Виды средних величин, условия их применения в экономическом анализе

ОБЩАЯ ТЕНДЕНЦИЯ (ТРЕНД) РЯДА ДИНАМИКИ. СТАТ. МЕТОДЫ ВЫЯВЛЕНИЯ И МАТ. ОЦЕНКИ ТРЕНДА ОСНОВНЫЕ МОДЕЛИ ОБЩЕЙ ТЕНДЕНЦИИ РД.

Общая тенденция развития явления во времени – это поступательное непрерывное изменение ур-ней РД за длит. Промежуток времени в опр. Направлении.

Тренд – это некот. аналит. ф-я, при пом. кот. описывают тенденцию РД.

Основные методы выявления общей тенденции:

Метод укрупнения интервалов. Данные за месяцы суммируются в квартАльные данные.

Метод скользящей средней (механического сглаживания). Замена факт. ур-ней РД средними арифм. ур-ми за опр. период.

Устанавливаются звенья: они должны составляться из числа ур-ней, отвечающих, напр., длительности внутригодовых циклов в изуч-м явлении (напр., даны кварталы за неск. лет, для них ск. ср. из 4-членных звеньев. Расчет: y ср.1=(y1+y2+y3+y4)/4; y ch.2=(y2+y3+y4+y5)/4 и т.п.

Для четного числа ур-ней кажд. знач.ср. ск. прих-ся на промежуток между 2мя смежными кватралами. Для опр-я сглаженных уровней пр-ся центрирование: для 3го кв. опр-ся срединное знач. между 1й и 2й ск. ср. (*первые 2 строки в таблице останутся пустыми*). Если нечетное число ур-ней, то центрировать не надо. Потом на график.

Метод аналитического выравнивания (построения трендовой модели). Подбор мат. функ-и, графич. линия кот. будет мах близка к граф. линии изуч-го РД.

Методика построения трендовой модели:

Факт. ур-ни РД изобр. На линейном графике.

По хар-ру расположения точек на графике подбираем мат. функ-ю.

Параметры ур-ний выч-ся по способу наименьших квадратов (*короче по формулам дальше, см. вторую их часть*)

а0=(суммаУ*сумма(tквадрат) – сумма(t*y)*сумма(t)) / n* сумма((t)квадрат) – (сумма t)квадрат)) = суммаУ / n = y ср.

a1=(n* сумма(t*y) - сумма(t)* суммаУ) / (n*сумма(tквадрат) – (сумма t)квадрат) = сумма(t*y) / сумма(tквадрат) = дельта ср.

Промежуточные расчеты. Есть упрощенный способ расчета параметров – способ отсета времени от условного нуля. За него берется середина РД. При четном числе – 2 средних значения берутся за – и +1, прибавляется по +-2, а если нечетное, то середина=0, прибавляется по +-1. Параметр а2= ср. коэф. Роста.

Вычисление параметров.

Вычисление теор. значений.- послед-но подставляем t в полученную тренд. модель.

Проверка правильности расчетов - сумма y ср. ti=сумма yi

Проверка адекватности тренд. модели.

Визуальная оценка – теор. ур-ни переносим на график.

Мат. оценка, произв. по стандартиз-й ошибке аппроксимации

G(дельта большая, как у дисперсии) y ср. ti = корень(сумма(yi-yti)квадрат / n)

11 Особенности сбора и обработки информации:

Для получения информации проводят статистические исследования.Стат.исслед.- ассовое систематическое научно-организованное наблюдение за явлением общ.жизни ко. Заключается в регистрации отобранных признаков у каждой единицы совокупности.

Получивинформацию,выявляют различные закономерности свойственные изучаемым явлениям.

Примеры сбора информации:- для определения числ.населения и его состава по полу,возрасту,образования, и т.д.Производит перепись населения.

- для выявления насколько удовлетворен спрос населения на конкретные товары проводят непосредственную регистрацию фактов реализован. И неудовлетворит. Спроса.

- для получения информ. О работе предприятия(выпускпоодукци, себестоимость, текучестькадров) организ. Ститистический учет на предприятиях.

Соотваетсвенно получают разного рода первичный стит. Материал:

-переписные листы в форме анкет-непосредств.записи регистраторов- установленные формы стит. Отчестности предприятий

Структурные средние:

Модой в статистике называют наиболее часто встречающееся в исследуемой совокупности значение признака. Мода широко используется в коммерческой практике при изучении покупательского спроса (при определении размеров одежды и обуви, которые пользуются широким спросом).

В интервальном вариационном ряду модой приближенно считают центральный вариант, т.н. модального интервала (с наибольшей частотой).

Моду определяют по формуле:

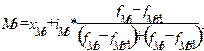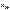где - начальное значение интервала, содержащего моду;

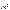- величина модального интервала;

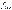- частота модального интервала;

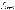- частота интервала, предшествующего модальному;

Медиана (Ме) – это величина, которая делит численность упорядоченного вариационного ряда на 2 равные части: одна часть значения варьирующая признака меньшие, чем средний вариант, а другая часть – большие. Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда, а с четным числом членов медианой будет средняя арифметическая из двух смежных вариант.

В интервальном вариационном ряду порядок нахождения медианы следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал.

Медиана делит численность ряда пополам, следовательно, она там, где накопительная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.

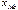где — начальное значение интервала, содержащего медиану;

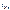— величина медианного интервала;

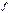— сумма частот ряда;

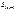— сумма накопленных частот, предшествующих медианному интервалу;

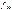— частота медианного интервала.

Средние величины – обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления.

При помощи средних происходит сглаживание различий в величине признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения. Средние имеют те же единицы измерения, что и признаки, по которым они вычисляются.

Виды средних величин:

- средняя арифметическая

- средняя гармоническая

- средняя агрегатная

- средняя квадратическая

- средняя геометрическая

- средняя хронометрическая

- структурные средние величины

Главная задача, перед проведением расчетов – выбор подходящей формулы из множества имеющихся. Формулы выбираются после тщательного изучения располагаемой информации.

Если надо вычислить среднюю не по абсолютным пок-ям, то следует найти «исходное соотношение средней» - записать формулу, по которой вычисляется данный относительный или средний показатель.

средняя арифметическая

а) простая (невзвеш.) – применяется для несгруппированных данных или если отдельные значения признака можно суммировать.

Х(средняя, сверху черта) = сумма(хi)/n (сумма х(i) – все значения признака, n – число наблюдений) – самое точное значение

б) средняя арифметическая взвешенная – применяется в рядах распределения для сгруппированных данных и в некоторых других случаях(когда известны x(i) и f(i))

X(средняя, сверху черта) = 1. (сумма xi)*fi/сумма fi – для дискретного ряда распределения

2. сумма x(i)`*f(i)/ сумма f(i) – для интервального ряда распределения.

средняя гармоническая

а) простая (невзвеш) – применяется, когда произведение вариантов (x(i) и частот (w(i)) равны между собой

X(средняя, сверху черта)= n/сумма (1/xi)

б) средняя гармоническая взвешенная – применяется в случаях, когда неизвестны частоты (f(i)), но известны варианты и произведение вариантов и частот.

X(средняя, сверху черта)=сумма wi/сумма(wi/xi)

средняя агрегатная - применяется в случаях, когда неизвестны варианты (xi), но известны частоты и произведение вариантов и частот.

X(средняя, сверху гориз черта)=сумма w(i)/сумма f(i)

средняя геометрическая – величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии.

X(средняя, сверху гориз черта)=(корень n-ой степени)П(x).

средняя квадратическая

х (ср.)= корень (сумма(х квадрат)/n) – среднее квадратическое отклонение

средняя хронометрическая

у (ср.)= (у0/2+у1+…+у(n-1)+уn/2) / (n-1) – чистая ср. хроном.

структурные средние величины – применяются для характеристики структуры рядов распределения, в дополнение к относительным и средним показателям (мода, медиана, квартили, децили…).

Модальная величина (мода) – значение признака, который чаще всего встречается в данной совокупности, т.е. наиболее типичн для нее. Мода широко используется в практике статистического анализа, например при изучении покупательского спроса, при регистрации цен и др.

В дискретном ряду распределения мода – вариант, имеющий наибольшую частоту.

В интервальном ряду используется следующая методика:

а) по f(max) определяется модальный интервал; б) определение моды по формуле Мо=Хо+i*(Fмо- Fмо-1/ ((Fмо- Fмо-1)+(Fмо- Fмо+1))); в) графический способ

Медиана – значение признака, который находится в середине ряда распределения, т.е. делит его на 2 равные части.

Соотношение между средней медианой и модой показывает направление ассиметрии ряда распределения. X(ср)<<=Me<=<Mo – левостор. (<<= - соотв. Варианты знаков)

Величины, приходящиеся на одной четверти и на трех четвертях расстояния от начала ряда, называются квартилями, на одной десятой – децилями, на одной сотой – процентилями.

14. Статистические показатели изучения тесноты связи Показ тесноты связи дают возможность охарактеризовать степень зависимости вариации результативного признака от вариации признака-фактора. При исследовании степени тесноты связи между качеств признаками, каждый из кот представлен в виде альтернатив признака, исполз коэф ассоциации или коэф контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой).

Ка=(ad-bc)/(ad+bc) - Чурпов; Кк =(ad-bc)/Ö(a+b)(b+d)(a+c)(c+d) - Пирсон.

Дата добавления: 2015-04-24