Малі вибірки. При розрахунку характеристик вибіркової сукупності (дисперсії, середньої і граничної похибок) передбачалось мати сукупність великого обсягу . В

При розрахунку характеристик вибіркової сукупності (дисперсії, середньої і граничної похибок) передбачалось мати сукупність великого обсягу 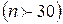. В науково-дослідній роботі та у практиці виробничих спостережень часто користуються вибірками невеликими за обсягом (в агрономічних і зоотехнічних дослідах, при перевірці якості продукції, в випадках, пов’язаних із знищенням зразків тощо). В статистиці вони називаються малими вибірками 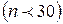. Вибірки з чисельністю понад 30 одиниць називають великими. Вони забезпечують більшу точність порівняно з малими вибірками. В статистиці доведено, що результати, отримані за малими вибірками, також поширюються на генеральну сукупність. Але тут виникають деякі особливості, які потрібно враховувати при обчисленні середнього квадратичного відхилення. При малому обсязі вибірки користуються незміщеною оцінкою дисперсії, яка позначається .

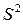Основи теорії малих вибірок були розроблені англійським математиком-статистиком В. Госсетом (псевдонім Стьюдент). Стьюдент показав, що для невеликого обсягу дисперсія у вибірці відрізняється від дисперсії у генеральній сукупності, що справедливо і для середніх квадратичних відхилень.

Середнє квадратичне відхилення генеральної сукупності є одним із параметрів кривої нормального розподілу. Тому використовувати функцію нормального розподілу для оцінки параметрів генеральної сукупності за даними малої вибірки в зв’язку з отриманням великих похибок не доцільно.

При обчисленні середньої похибки за невеликими вибірками завжди потрібно користуватись незміщеною оцінкою дисперсії:

,

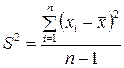де – число ступенів свободи варіації 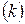, яким називають число одиниць, що можуть приймати довільні значення, не змінюючи їх загальної характеристики (середньої).

Нехай проведено п’ять спостережень: 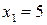; ; 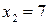; ; 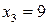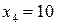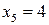. Середня величина визначається за формулою середньої арифметичної простої:

.

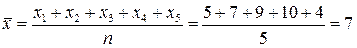Отже, вільно варіюючи величин залишається тільки чотири. Тому що п’яту можна знайти за відомими чотирма величинами і середньою:

.

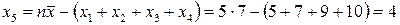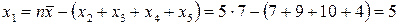і т.д.

Для даного прикладу число ступенів свободи варіації дорівнює:

.

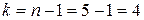Стьюдентом було обґрунтовано закон розподілу відхилень вибіркової середньої від генеральної середньої для малих вибірок. Згідно розподілу Стьюдента ймовірність того, що гранична похибка не перевищить 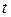– кратну середню похибку в малих вибірках, залежить від величини 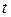і чисельності вибірки .

Теоретичне нормоване відхилення для малих вибірок одержало назву 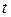– критерію Стьюдента на відміну від 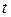– критерію нормального розподілу, який використовується у великих вибірках. Значення 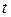– критерію Стьюдента табульовані і представлені в спеціальних таблицях (дод. Д).

Порядок визначення середньої і граничної похибки для малої вибірки покажемо на прикладі.

Приклад. Для сушіння зерна на пункті прийому у господарстві формують партію зерна озимої пшениці. Для того, щоб задати потрібний режим роботи зерносушарки, необхідно визначити вологість зерна. Для цього протягом дня з автомашин взяли вибірково 10 проб на вологість зерна, що поступило від комбайнів. Величини вологості зерна представлена в табл. 5.

Таблиця 5

Вологість зерна озимої пшениці

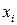
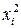
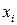
Номер проби	Вологість зерна, %	Квадрат вологості,	Номер проби	Вологість зерна, %	Квадрат вологості,
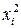
	17,0	289,00		17,5	306,25
	17,4	302,76		18,4	338,56
	18,4	338,56		19,0	361,00
	17,7	313,29		18,6	345,96
	18,5	342,25		19,5	380,25
Х	Х	Х	Разом	182,0	3317,88

Визначити: 1) середню вологість зерна озимої пшениці за вибіркою; 2) середню і граничну похибки вибіркової середньої вологості зерна; 3) довірчий інтервал, в якому перебуває середня вологість зерна у генеральній сукупності. Довірчу ймовірність взяти рівною .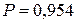

Середня вологість зерна озимої пшениці складає:

.

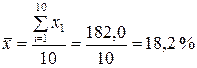Спостерігаючи за окремими спостереженнями бачимо, що вологість зерна варіює і середня лише по 10спостереженнях матиме деяку похибку.

Обчислимо вибіркову дисперсію:

.

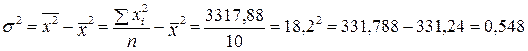Вибіркову дисперсію скоригуємо на втрату числа ступенів свободи, тому що чисельність вибірки 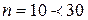одиниць. Скоригована дисперсія дорівнюватиме:

.

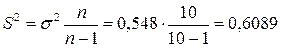Незміщену оцінку дисперсії можна визначити і за такою формулою:

.

.

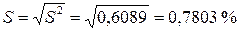Визначимо середню похибку вибіркової середньої вологості зерна:

.

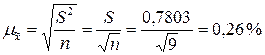Отже, середня вологість зерна озимої пшениці у генеральній сукупності дорівнює 18,2% при середній похибці вибіркової середньої 0,26%. Це значить, що 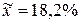є точковою оцінкою генеральної середньої з похибкою 0,26%.

Для одержання інтервальної оцінки генеральної середньої і побудови довірчого інтервалу визначимо граничну похибку вибіркової середньої вологості зерна для малої вибірки. Для цього за таблицею «Значення критерію Стьюдента» (дод. Д) при заданому рівні ймовірності 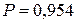(рівень істотності 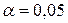) і відповідному числі ступенів свободи варіації 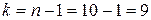знайдемо табличне (теоретичне) значення критерію Стьюдента .

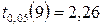Гранична похибка вибіркової середньої є точковою оцінкою генеральної середньої і дорівнює:

.

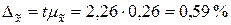Дамо інтервальна оцінку середнього відсотка вологості зерна озимої пшениці в генеральній сукупності, записавши довірчий інтервал:

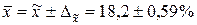, або

;

;

.

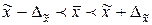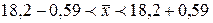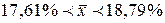Отже, з довірчою ймовірністю 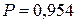можна стверджувати. Що середня вологість зерна в генеральній сукупності буде перебувати в межах від 17,61% до 18,79%.

Дата добавления: 2015-05-10