М'які та жорсткі біфуркації. Теорія катастроф

Саме слово "біфуркація" означає роздвоєння. Але що ж таке на справді біфуркація? Біфуркація – це явище, коли система втрачає свою стійкість при плавній змінні деяких її параметрів. А точки, де відбуваються такі зміни називаються точками біфуркації. Біфуркація насамперед може бути м’якою та жорсткою. М’яка – це коли стан системи після втраті стійкості не дуже сильно змінився від попереднього стану. Жорстка біфуркація – це навпаки, коли система різко змінює свій стан при втраті стійкості.

Для ясності можна розглянути два приклади. Нехай задана деяка потенціальна функція, що залежить від параметра u, а точка u=u* є точкою біфуркації.

Якщо система при переході через таку точку втрачає свою стійкість і переходить у новий стан, досить близький до попереднього (рис.1) то це буде м’яка біфуркація. Як показано на рисунку, таких станів може бути навіть кілька, але всі вони розміщені відносно недалеко, від попереднього.

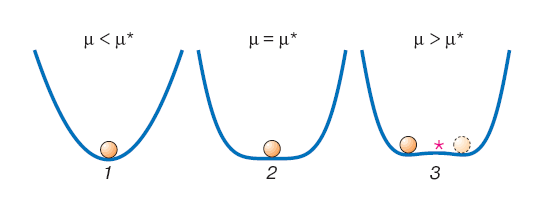
Рис. 1. М’яка біфуркація.

Якщо система різко змінює свій стан (рис.2) то ця біфуркація буде жорсткою. Як правило при жорсткій біфуркації має існувати, недалеко від стійкого, деяке нестійке положення (на рис. 2(1), відмічено *).

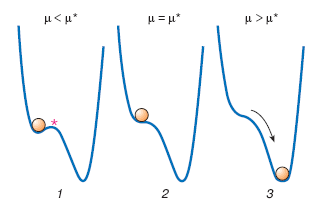
Рис. 2. Жорстка біфуркація.

І саме такі – жорсткі – біфуркації стали основою для теорії катастроф. Точки, де система різко змінює свій стан, або і взагалі може зазнати свого краху.

Теорія катастроф. Ми знаємо, що зміни як і у природі так і всюди, можуть бути як плавними, так і стрибкоподібними. Наприклад, поставили кип’ятити воду: спочатку все йде плавно і гладко, а потім враз з’являються бульбашки, пара. Або землетрус: здається все йде як завжди, як раптом починають валитися будинки, утворюватися в землі тріщини. Або візьмемо якогось верблюда: якщо навантажимо його масою в n кілограм, то нічого не станеться, а коли n+1 – то може зламатися його спина.

Катастрофою називається втрата системи стійкості або ж, якщо бути точнішим, стрибкоподібна змінаїї стану, викликана при плавній зміні зовнішніх умов. А математична теорія, що аналізує поведінку динамічних систем при змінні її параметрів, – теорією катастроф.

Як впізнати катастрофу. І ще одним коренем теорії катастроф була теорія особливостей – грандіозне узагальнення досліджень функцій на точки екстремуму, тобто особливі точки. Чому саме теорія особливостей? Тому, що точки катастроф – це деяка підмножина особливих точок певної системи.

Володіючи такими знаннями давайте дослідимо на наявність точок катастроф дві функції: у = х² та у = х³. Легко побачити, що як в першої, так і в другої функції буде одна особлива точка х = 0. Але вони залежать тільки від х, тому введемо у наші функції невелике збурення – параметр ε, і нехай наші функції набудуть наступної форми:у = х² – εх та у = х³ – εх. У першому випадку (у = х² – εх) особливою точкою буде точка х = ε. Тобто при невеликих значеннях ε система мало зміниться від початкової. А якщо взяти нашу функцію, як потенціальну функцію деякої системи (рис. 3(а)), то легко помітити, що при невеликій зміні ε, стійкий стан системи мало відрізнятиметься від попереднього. Отже у цій функції точки катастрофи нема.

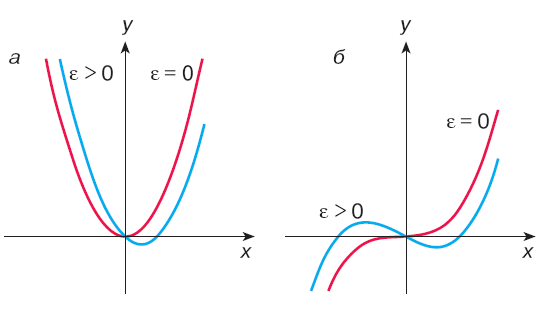
Рис. 3. Особливі точки.

Зовсім інша річ буде, якщо взяти функцію у = х³ – εх. Тут особливими точками будуть х = ± √ε. При ε > 0 здавалосьби все нормально – стійкий стан (локальний мінімум) мало зміниться від попереднього, але якщо взяти ε< 0 тоді наша система катастрофічно зміниться – не буде ніякої особливої точки, ніякого стійкого стану. Система різко і якісно змінить свій стан. Тому, у цьому випадку, точка х = 0 буде точкою катастрофи.

Основні типи катастроф. Їх є сім:катастрофа складки, катастрофа збірки, катастрофа ластівчиного хвоста, катастрофа метелика, еліптична омбіліка, гіперболічна омбіліка, параболічна омбіліка. Розглянемо їх по черзі.

Катастрофа складки. Має вигляд 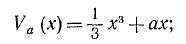. Вона має лише одну точку катастрофи при х = 0, один внутрішній (х) і один керуючий (а) параметри.

Катастрофа збірки. Має вигляд 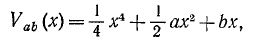. Вона уже має криву катастрофи і одну точку повернення, один внутрішній (х) і два керуючі (а, b) параметри. Разом із катастрофою складки – одні із найбільш поширених катастроф. Тобто найчастіше зустрічається як у світі, так і при різних експериментах та дослідах.

Катастрофа ластівчиного хвоста. Має вигляд 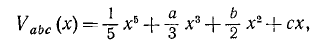. Вона має теж криву катастрофи, що дуже нагадує ластівчин хвіст при а < 0. Має один внутрішній (х) і три керуючі (а,b,с) параметри.

Катастрофа метелика. Має вигляд 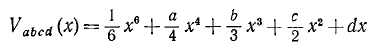. Вона має криву катастрофи, що дуже нагадує метелика при а < 0 і b = 0. Має один внутрішній (х) і чотири керуючі (а,b,с,d) параметри.

Еліптична омбіліка. Має вигляд 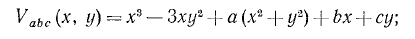. Має два внутрішніх (х,у) і три керуючих (а,b,с) параметри.

Гіперболічна омбіліка. Має вигляд . Має два внутрішніх (х,у) і три керуючих (а,b,с) параметри.

Параболічна омбіліка. Має вигляд 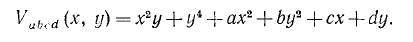. Має два внутрішніх (х,у) і чотири керуючі (а,b,с,d) параметри.

Омбілічні катастрофи – це катастрофи другого порядку. Вони часто зустрічаються в оптиці при відображенні світла від тривимірної поверхні. Самі по собі такі катастрофи тісно зв’язані з геометрією майже сферичних поверхонь. А Рене Том пропонував розглядати гіперболічну омбілічну катастрофу як процес руйнування хвилі, а еліптичну омбілічну катастрофу – створення структур, подібних на волосяне покриття.

Дата добавления: 2015-05-08