Біфуркація Хопфа

Біфуркації положення рівноваги

Параметричні діаграми

Існує три біфуркації положення рівноваги:

1. злиття двох станів рівноваги в один – ẋ = λ – x²

2. народження граничного циклу – ẋ = λx – x²

3. поява трьох станів рівноваги з одного –ẋ = λx – x³

1. Біфуркація “сідло–вузол” (дотична, катастрофа складки)x_n+1 = λ – x_n²

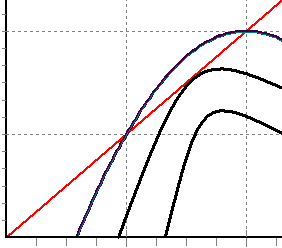
2. Біфуркація Хопфа (транскритична, народження граничного циклу)x_n+1=λx_n–x_n²

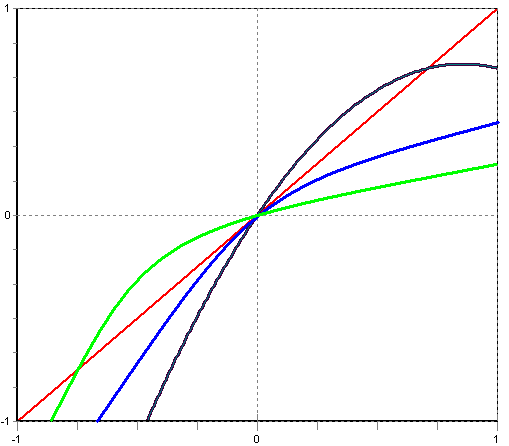
3. Біфуркація “Вила” (суперкритична, втрата симетрії)x_n+1 = λx_n – x_n³

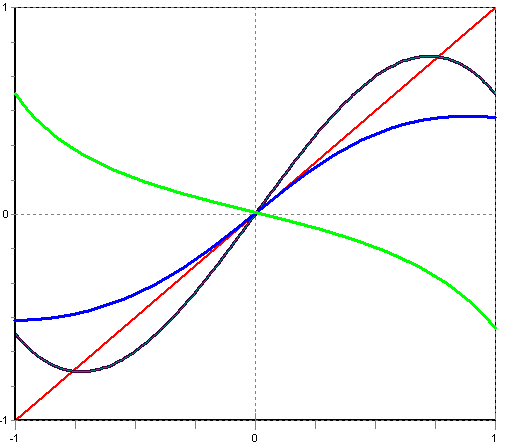
Біфуркація Хопфа – біфуркація, при якій стаціонарна точка втрачає стійкість.

При біфуркації Хопфа втрата стійкості дисипативною системою локальна, тому фазові траєкторії залишаються в околі точки рівноваги, що означає виникнення в цьому околі граничного циклу. Як наслідок, в диспативній ситемі виникають автоколивання.

На рисунку показано, як змінюється характер фазового портрету при біфуркації Хопфа. На перших трьох діаграмах параметри дисипативної системи такі, що точка рівноваги стійка, фазові траєкторії збігаються до неї, але при цьому виконують дедалі більше обертань. Фізично це відповідає дедалі повільнішому затуханню коливань. При переході через точку біфуркації навколо точки рівноваги виникає граничний цикл. Фазові траєкторіїї збігаються до цього циклу як зовні, так і з середини. Така ситуація відповідає автоколиванням, що підтримуються однаковими й не затухають.

Крім описаної біфуркації, яку називають надкритичною, існує ще підкритична біфуркація Хопфа. При цій біфуркації виникає нестійкий граничний цикл. У цьому випадку нестійкий фокус перетворюється в стійкий, і навколо нього виникає невеликий басейн притягання. Басейн притягання обмежений нестійким граничним циклом, від якого фазові траєкторії розбігаються всередину до вже стійкого фокуса й назовні – до інших атракторів.

Х

(x₀,y₀)

λ < 0

Х

λ > 0

Y

Y Y Х  

Рис. 2. Фокус і граничний цикл. Т

На рисунку зображено перетворення стійкого вузла у граничний цикл (і навпаки) при переході параметра λ через нуль. Система втрачає рівновагу і виходить на режим періодичних коливань. Це і є біфуркація Хопфа. Особливістю цього її різновиду є "м’яке" (неперервне) збудження системи при плавному зростанні параметра λ, що продемонстровано на наступному рисунку:

–1

–2

λ

радіус граничного циклу

Рис. 5. “м’яке” збудження системи за біфуркації Андронова–Хопфа за біфуркації Андронова–Хопфа   за біфуркації Андронова–Хопфа   за біфуркації Андронова–Хопфа

Відповідно біфуркації даного типу також отримали назву "м’яких".

Існує й інший – жорсткий режим збудження системи. Запишемо систему:

Це також різновиж біфуркації Хопфа. Стаціонарними траєкторіями системи будуть фокус і два граничних цикла:

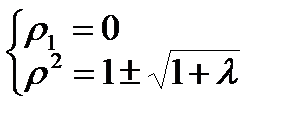
Отже фазовий портрет системи залежатиме від параметра λ дещо інакше:

Х

λ <–1

Y

Х

λ > 0

Y

Х

–1 < λ < 0

Y

Для λ<–1 за будь–яких початкових умов система виходить на стійкий стаціонарний стан – коливань немає.

На інтервалі –1<λ< 0 з’являється ще два атрактора – внутрішний і зовнішний граничні цикли, перший з яких нестійкий. Всі траєкторії сходяться або у фокус, або до зовнішнього циклу, через що даний ефект Вінфрі (Winfree) назвав "чорною дірою".

Перехід через точку λ= 0 призводить до втрати стійкості фокусом ρ=0, що супроводжується стрибкоподібним перенаправленням траекторій до зовнішнього граничного циклу. У системі миттєво починаються коливання скінченої амплітуди. Таке її збудження має різкий "жорсткий" характер, що і зумовило його назву "катастрофа".

–1

–2

λ

радіус граничного циклу

Рис. 7. “жорстке” збудження системи

зовнішний цикл

внутрішний цикл

Завдяки Рене Тому дослідження "жорстких" біфуркацій розвинулось у самостійну теорію катастроф. Незважаючи на всю складність її математичного апарату, життєва значимість терміну "катастрофа" призвела до широкої популярності цієї теорії і відповідного її трактування не тільки в інших наукових галузях, а й у науково–фантастичній літературі, засобах масової інформації, тощо.

51.Біфуркація "сідло–вузол"

Попередній приклад (питання 56) показав, що неперервна зміна параметра може супроводжуватись більше, ніж однією біфуркацією системи. Зараз ми продемонструємо, що у цьому ланцюжку можуть зустрічатися й різнотипні біфуркації. Розглянемо просту систему

ẋ₁ = –x² + λ

ẋ₂ = –x²

При λ = 0, система має одну особливу точку сідло–вузол. При збільшенні λ вона розділяється на дві – сідло і вузол:

Рис. 8. Біфуркація сідло–вузол.

Х

Y

Дата добавления: 2015-05-08