Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона

Во многих случаях закон распределения изучаемой случайной величины неизвестен, но есть основания предположить, что он имеет вполне определенный вид: нормальный, биноминальный или какой другой. Пусть необходимо проверить гипотезу Н₀ о том, что СВ Х подчиняется определенному закону распределения, заданному функцией распределения F(x).

Пусть х₁,х₂, …,х_n - выборка наблюдений случайной величины X. Проверяется гипотеза Н₀ о том, что случайная величина X имеет функцию распределения F(x).

Требуется сделать заключение: согласуются ли результаты наблюдений с высказанным предположением, для этого используется специально подобранная величина – критерий согласия. Критерием согласия называется статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Он используется для проверки согласия предполагаемого вида распределения с опытными данными на основании выборки.

Существуют различные критерии согласия: Пирсона, Колмогорова, Фишера, Смирнова. Критерий согласия Пирсона – наиболее часто употребляемый критерий для проверки гипотезы о законе распределения.

Критерий согласия Пирсона (χ²):

Разбиваем область значений СВ Х на m интервалов. Составляем эмпирический ряд распределения (Δ_i/n_i) и теоретический ряд распределения (Δ_i/n^T_i), где теоретические частоты определяются равенством: n^T_i=n·p_i, здесь вероятность p_i вычисляется в предположении рассматриваемого распределения.

Если эмпирические частоты n_i сильно отличаются от теоретических n^T_i, то проверяемую гипотезу Н₀ следует отвергнуть, в противном случае – принять.

В качестве меры расхождения между эмпирическими и теоретическими частотами К. Пирсон (1857-1936, англ. математик) предложил величину («критерий Пирсона»):

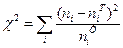
Согласно теореме Пирсона при n→∞ статистика χ² имеет распределение с

k=m-r-1 степенями свободы (m- число интервалов, r – число параметров предполагаемого распределения).

Дата добавления: 2015-05-08