Методи прямого пошуку

1.1.1. Загальна характеристика методів прямого пошуку

Методи прямого пошуку — це методи, у яких використовуються тільки значення цільової функції (методи нульового порядку). Розглянемо наступні методи, засновані на евристичних міркуваннях. Ці методи досить часто застосовуються на практиці, дозволяючи в ряді випадків одержати задовільні розв'язання.

Основна перевага методів нульового порядку полягає в тому, що вони не вимагають безперервності цільової функції й існування похідних.

1.1.2. Метод конфігурацій (метод Хука й Дживса).

Ідея методу Хука-Дживса

Алгоритм містить у собі два основних етапи пошуку.

1. На початку досліджується окіл обраної точки (базисної точки), в результаті чого обирається прийнятний напрямок спуску.

2. У визначеному напрямку знаходиться точка з найменшим значенням цільової функції. Ця точка обирається в якості нової базисної точки.

Ця процедура триває доти, поки на околах базисних точок вдається знаходити прийнятні напрямки спуску.

Схема алгоритму методу Хука-Дживса

Крок 1.

Задаються:

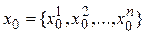— початкове наближення (перша базисна точка);

h — початковий крок для пошуку напрямку спуску;

d — точність розв'язання (граничне значення для кроку h);

λ — множник прискорення.

Покласти к =0.

Крок 2. (Перший етап).

Визначається напрямок мінімізації цільової функції 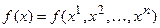у базисній точці 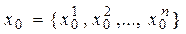. Для цього послідовно дають приріст змінним 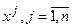у точці х_к.

Покласти z = x_k.

Циклічно давати приріст змінним x^j і

якщо f(z)<f(x_k), формуємо ,

якщо ж ні, то

якщо f(z)<f(x_k) ,,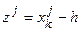

інакше z^(j)=x_k^(j).

Так для всіх j(j=1,2,...,n).

Крок 3.

Якщо z=x_k, тобто не визначився підходящий напрямок, то обстеження околиці базисної точки х_к повторюється, але з меншим кроком h (наприклад, h=h/2).

Якщо h>d, то перейти до кроку 2, тобто повторити обстеження точки хк.

Якщо h<d, то пошук закінчується, тобто досягнуте граничне значення для кроку h і знайти прийнятний напрямок спуска не вдається. У цьому випадку покладається

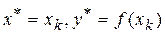
Крок 4. (Другий етап).

Якщо z ¹ x_k, то потрібно знайти нову базисну точку в напрямку вектора z–x_k: x_{k +1}= x_k + l (z – x_k), де l — коефіцієнт «прискорення пошуку».

Визначається таке значення l=l_к, при якому досягається найменше значення цільової функції в обраному напрямку, тобто функції

f(x_k +l(z-x_k) = j(l).

Залежно від способу вибору l_к можливі варіанти методу:

а) l_к = l =const постійного для всіх ітерацій;

б) задається початкове l ₀= l, а далі l_к = l_{к -1}, якщо f(x_k+1)<f(x_k), інакше дробимо l_к, поки не виконається ця умова;

в) l_к визначається розв'язанням задачі одномірної мінімізації функції j(l).

У такий спосіб визначається нова базисна точка x_k+1=x_k + l(z-x_k). Приймаємо к=к+1 і пошук оптимального розв'язання повторюється із кроку 2.

Дата добавления: 2015-05-23