Метод симплекса

Під симплексом розуміється n -мірний опуклий багатогранник n -мірного простору, що має n +1 вершину. Для n =2 це трикутник, а при n =3 це тетраедр.

Ідея методу полягає в порівнянні значень функції в n +1 вершинах симплекса й переміщенні симплекса в напрямку кращої точки. У розглянутому методі симплекс переміщається за допомогою операцій відбиття. Далі прийнятo наступне: х ₀(k), х ₁(k), …, х_n (k) — вершини симплекса, де к — номер ітерації.

Рис.

1. Побудова нового симплекса

Схема алгоритму методу симплекса

Крок 1. Побудова початкового симплекса.

Для цього задаються початкова точка х₀(0) і довжина ребра симплекса l. Формуються інші вершини симплекса: x_i(0) = x₀(0) + l*e_i (i=1,2,…,n),де e_i – одиничні вектори.

Рис.

2. Побудова початкового симплекса

Крок 2. Визначення напрямку поліпшення розв'язання.

Для цього на к -й ітерації обчислюються значення цільової функції в кожній точці симплекса. Нехай для всіх i:

,

де min, max, i — номера відповідних вершин симплекса. Визначимо центр ваги всіх точок, крім точки x _max(k),

.

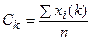Тоді напрямок поліпшення розв'язання визначається вектором

C_k – x _max(k).

Крок 3. Побудова відображеної точки.

Заміна вершини x _max(k) з максимальним значенням цільової функції на нову точку за допомогою операції відображення, результатом якої є нова точка:

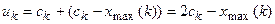
Рис.

3. Побудова відображеної точки

Крок 4. Побудова нового симплекса.

Обчислюємо f (u_k). При цьому можливий один із двох випадків:

а) ;

б) .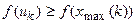

Випадок а): вершина x _max заміняється на u_k, чим визначається набір вершин (к +1)-й ітерації й к -я ітерація закінчується.

Випадок б): у результаті відображення отримується нова точка u_k, значення функції в якій ще гірше, ніж у точці x _max, тобто відображати симплекс нікуди. Тому в цьому випадку виконується пропорційне зменшення симплекса (наприклад, в 2 рази) в бік вершини x _min(k):

,

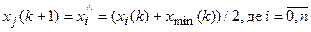На цьому к -я ітерація закінчується.

Крок 5. Перевірка збіжності.

Якщо

,

то пошук мінімуму закінчується й приймається

.

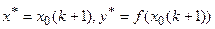У противному випадку к = к +1 і відбувається перехід до кроку 2.

Рис.

4. Схема алгоритму методу симплекса

1.1.4. Метод деформуючого симплекса (метод Нелдера-Міда).

Метод деформуючого симплекса більш загальний і дозволяє враховувати локальні властивості поверхні цільової функції. Симплекси витягаються в напрямку нахилу поверхні, їхні осі повертаються при зустрічі з яром на поверхні цільової функції, поблизу мінімуму вони стискуються.

Симплекс переміщається за допомогою трьох основних операцій над симплексом: відбиття, розтягання й стиск.

Схема алгоритму методу Нелдера-Міда

Крок 1. Побудова початкового симплекса.

Задаються:

х₀(0) — початкова точка

l — довжина ребра.

Формуються інші вершини симплекса:

x_i (0)= x ₀(0)+ le_i (i =1, 2, …, n),

де e_i — одиничні вектори.

Крок 2. Визначення напрямку поліпшення розв'язання.

На кожній ітерації обчислюються значення цільової функції в кожній вершині симплекса. Нехай для всіх i

де min, m, max, i — номера відповідних вершин симплекса. Визначимо центр ваги всіх точок, крім точки x _max(k),

Тоді напрямок поліпшення розв'язання визначається вектором

Крок 3. Побудова нового симплекса.

Заміна вершини x _max(k) з максимальним значенням цільової функції на нову точку за допомогою операції відбиття, результат якої є нова точка , де a — коефіцієнт відображення.

Рис.

Крок 4. Побудова нового симплекса.

Обчислюємо f (u_k), при цьому можливо один із трьох випадків:

а) f (u_k)< f (x _min(k));

б) f (u_k)> f (x_m (k));

в) f (x _min(k)) f (u_k) f (x_m (k)).

Випадок а): відбита точка є точкою з «найкращим» значенням цільової функції. Тому напрямок відбиття є перспективним і можна спробувати розтягти симплекс у цьому напрямку. Для цього будується точка

,

де b >1 — коефіцієнт розтягнення.

Якщо 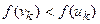, то вершина x _max(k) заміняється на v_k, у противному випадку на u_k і k -а ітерація закінчується.

Випадок б): в результаті відображення отримується нова точка u_k, яка, якщо замінити x _max(k), сама стане «найгіршою». Тому в цьому випадку виконується стиск симплексу. Для цього будується точка v_k:

де 0<γ<1 — коефіцієнт стиску.

Рис.

5. Побудова нового симплекса

Якщо , то вершина x _max(k) заміняється на v_k.

У противному випадку вершинам x_i (k +1) (i =0, 1, 2, …, n) привласнюється значення:

і на цьому k -а ітерація закінчується.

Випадок в): вершина x _max(k) заміняється на u_k, чим визначається набір вершин (k +1)-ї ітерації та k -а ітерація закінчується.

Шаг 5. Перевірка збіжності.

Якщо

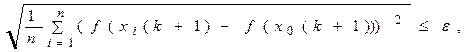
то пошук мінімуму закінчується й покладається

.

У противному випадку к = к +1 і відбувається перехід до кроку 2.

Досвід використання описаного алгоритму показує, що доцільно брати наступні значення параметрів:

a =1, b =2, g =0.5.

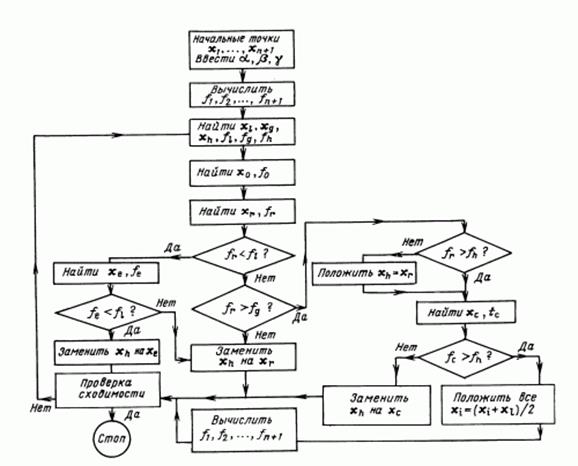
Рис. 6.

Алгоритм методу Нелдера-Міда

Дата добавления: 2015-05-23