Алгоритм методу Розенброка

Метод обертових координат (метод Розенброка)

Ідея методу полягає в обертанні системи координат відповідно до зміни швидкості спадання цільової функції. Нові напрямки координатних осей визначаються таким чином, щоб одна з них відповідала напрямку найбільш швидкого спадання цільової функції, а інші знаходяться з умови ортогональності. Алгоритм методу полягає в наступному (рис. 7).

Рис.

7. Геометрична інтерпретація методу Розенброка

З початкової точки х ₀ здійснюють спуск у точку х ₁ по напрямках, паралельним координатним осям. На наступній ітерації одна з осей повинна проходити в напрямку y₁ = х ₁– х ₀, а інша — у напрямку, перпендикулярному до в₁. Спуск уздовж цих осей приводить у точку х ₂, що дає можливість побудувати новий вектор х ₂– х ₁ і на його базі нову систему напрямків пошуку. У загальному випадку даний метод ефективний при мінімізації яружних функцій, тому що результуючий напрямок пошуку прагне розташуватися уздовж осі яру.

Крок 1

Позначають через 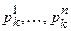напрямки координатних осей у деякій точці х_k (на к -й ітерації). Виконують пробний крок h ₁ уздовж осі , тобто

.

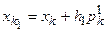Якщо при цьому , то крок h множать на величину b >1;

Якщо , - то на величину (- b), 0 < | b | < 1;

.

Приймаючи ?h ₁= а ₁.одержують

.

Крок 2

З точки виконують крок h ₂ уздовж осі :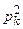

.

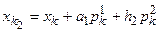Повторюють операцію кроку 1, тобто

.

Цю процедуру виконують для всіх інших координатних осей. На останньому кроці одержують точку

.

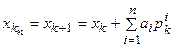Крок 3

Вибирають нові осі координат . В якості першої вісі приймається вектор

.

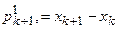Інші вісі будують ортогональними до першої вісі за допомогою процедури ортогоналізації Грама-Шмідта. Повторюють обчислення з кроку 1 до виконання умов збіжності.

Коефіцієнти b підбираються емпірично. Гарні результати дають значення b = –0,5 при невдалих пробах і b =3 при вдалих пробах .

На відміну від інших методів нульового порядку алгоритм Розенброка орієнтований на відшукання оптимальної точки в кожному напрямку, а не просто на фіксоване зрушення в усіх напрямках. Величина кроку в процесі пошуку безупинно змінюється залежно від рельєфу поверхні рівня. Сполучення обертання координат з регулюванням кроку робить метод Розенброка ефективним при розв'язанні складних задач оптимізації.

Дата добавления: 2015-05-23