Метод ковзної середньої

Метод ковзної середньої є найбільш простим способом згладжування емпіричних кривих. Суть цього методу складається в заміні фактичних значень показника їхніми усередненими величинами, що мають значно меншу варіацію, чим вихідні рівні ряду.

Залежно від періоду усереднення розрізняють ковзні середні, розраховані для непарного й парного числа інтервалів часу. Розглянемо порядок побудови ковзної середньої з непарним числом членів.

Є динамічний ряд, що складається з рівнів y₁, y₂, y₃, …, y_n.

Для визначення ковзної середньої послідовно розраховують суми m елементів ряду (де m – непарне число), поступово переходячи від перших членів y₁, y₂, y₃, …y_n до наступних груп рівнів: y₂, y₃, …y_m+1; y₃, y₄, …y_m+2; y₄, y₅, …y_m+3; і т.д.

По окремих сумах визначають середні арифметичні, кожна з яких міняє свою величину («ковзає») у міру збільшення параметра t. Із середніх арифметичних формується новий динамічний ряд, елементи якого в значній мірі вільні від випадкових зовнішніх впливів на прогнозований показник. Вважається, що ковзні середні більш точно характеризують тенденцію зміни ознаки, чим рівні вихідного тимчасового ряду. Найбільше часто на практиці застосовуються трьох- і п’ятичленні середні.

Їхній розрахунок ведеться по формулах

y_t′ = (y_t-1 + y_t + y_t+1)/3, t=2,3…,(n–1);

14y_t′ = (y_t-2 + y_t-1 + y_t + y_t+1+ y_t+2)/5, t=3,4…,(n–2),

де y_t′ – ковзна середня.

Більш складна обчислювальна схема використовується в тих випадках, коли ковзна середня визначається по парному числу елементів. При парному періоді згладжування проста середня арифметична має один істотний недолік – вона не може бути приписана жодному реальному значенню t, оскільки доводиться на проміжок часу між двома роками. Наприклад, при t = 4 середня арифметична буде ставитися до проміжку між другим і третім роком; при m=6 –до проміжку між третім і четвертим роком і т.д.

При виконанні реальних розрахунків ковзну середню з парним періодом вирівнювання визначають у два етапи. Спочатку знаходять середні для проміжків часу (t–1 й t, t й t+1), а потім отримані величини підсумують і знову використають для розрахунку середньої.

З ковзних середніх з парним числом елементів найчастіше використається згладжування по чотирьох рівнях динамічного ряду. Обчислення чотиричленної ковзної середньої здійснюється по формулі

,

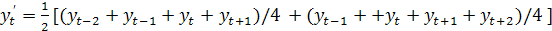t=3,4…,(n–2),

Застосування ковзних середніх дозволяє «вирівняти» контури вхідної кривої, що створює умови для більш точного відтворення динаміки зміни показника.

Приклад 1. Перевірка наявності тенденції

Дослідити часовий ряд на наявність тренду (тенденції). Умовні дані про витрати на впровадження інновацій в попередньому періоді, тис грн. (Y).

Вхідні дані та обчислення оформимо у таблиці (табл. 7.1).

Таблиця 7.1

t (рік)	X
Витрати на впровадження інновацій в попередньому періоді, тис грн.	Y	3,52	9,7	8,9	9,8	10,1	13,9	19,9	14,3	11,5	19,5	14,2
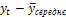
	-9,52	-3,34	-4,14	-3,24	-2,94	0,86	6,86	1,26	-1,54	6,46	1,16
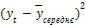
	90,63	11,16	17,14	10,50	8,64	0,74	47,06	1,59	2,37	90,63	11,16

Продовження таблиці 7.1

	20,2	22,7	28,2	25,2		24,3	21,5	27,1	36,3	34,1	34,1	35,2	44,5
0,96	7,16	-7,15	-1,65	-4,65	-4,85	-5,55	-8,35	-2,75	6,45	4,25	4,25	5,35	14,65
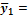
	13,04		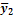									=	29,85
41,73	1,35	0,92	51,27	51,12	2,72	21,62	23,52	30,80	69,72	7,56	41,60	18,06	18,06

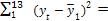285,09 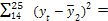528,05

Обчислення:

Крок 1. Вхідний часовий ряд у₁ , у₂, у₃, …, у_л розбиваємо на дві приблиз­но рівні частини обсягом п₁ ≈ п₂: п₁ = 13, п₂ = 12, (п₁ + п₂ = п);

Крок 2. Для кожної з частин обчислюють середні значення та дис­персії:

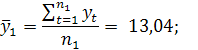
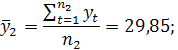
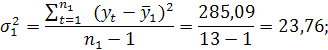
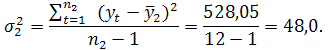
Крок 3. Висуваємо основну гіпотезу про рівність середніх значень:

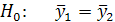
проти альтернативної .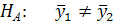

Нульову гіпотезу відхиляємо: .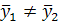

Та допоміжну гіпотезу про рівність дисперсій

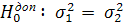
проти альтернативної .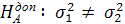

Допоміжну нульову гіпотезу про рівність дисперсій відхиляємо: .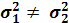

Крок 4. Перевіряємо допоміжну гіпотезу за допомогою F-критерію Фішера. Для цього порівняємо розрахункове (експериментальне) зна­чення критерію з табличним (критичним) значенням розподілу Фішера:

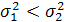, тому

F_табл = F(а, k₁,k₂) = 2,79,

при a=0,05 – заданий рівень значущості, k₁= п₁ –1=13–1=12, k₂= п₂ –1=12–1=11.

За критерієм Фішера F_експ < F_табл. Переходимо до наступного пункту.

Крок 5. Основну гіпотезу про відсутність тренда перевіряють за допомогою
t-критерію Стьюдента. Обчислимо вибіркову статис­тику – розрахункове значення критерію Стьюдента за формулою

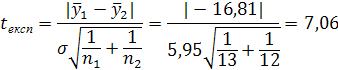
де s – середньоквадратичне відхилення різниці середніх;

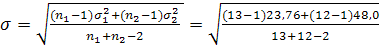= 5,95

t_табл = 2,18,

де t_табл =t(а, (п– 2)).

Розрахункове значення t_експ > t_табл. Основна гіпоте­за Н₀відхиляється. Отже, ряд має тренд.

Висновок. Нульова гіпотеза (H₀) відхиляється, ряд має тенденцію до змінювання (тренд є).

Приклад 2. Згладжування емпіричних кривих

Провести вирівнювання за методом трьох- чотирьох- та п’ятичленної ковзної середньої.

Нижче представлена інформація про розміри балансового прибутку (у млн. грн.), отриманою групою заводів первинного виноробства за період з 1996 по 2008 р. Нанести вихідні дані на графік.

Всі обчислення оформимо у вигляді таблиці (табл. 7.3).

Таблиця 7.3.

Рік (t)	Розмір балансового прибутку yt, млн. грн.	Тричленні суми	Тричленні ковзні середні yt’	Чотиричленні суми	Проміжні середні	Чотирьох-членні ковзні середні	П’ятичленні суми	П’ятичленні ковзні середні yt’
			274,3
			329,3		305,75			314,4
			332,3		334,25	320,0
			384,0		350,00	342,1		356,2
			377,7		383,25	366,6
			415,3		398,75	391,0		402,4
			420,0		415,75	407,3		417,6
			434,7		421,25	418,5		423,6
			425,0		434,25	427,8		435,6
			433,0		429,00	431,6		427,8
			432,3		430,50	429,8

Нанесемо вихідні дані на графік (рис. 7.3). Як видно з малюнка, розмір балансового прибутку коливається в значному діапазоні. Зробимо статистичне вирівнювання вихідного ряду.

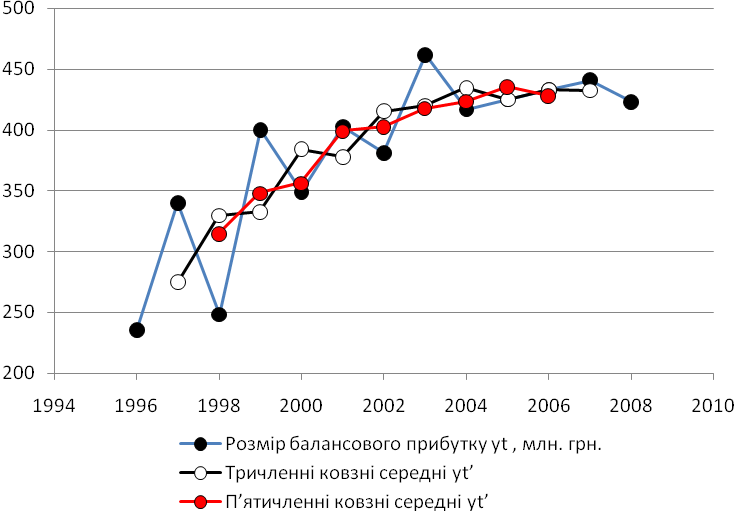
Рис. 7.3. Вхідна крива й ковзні середні

Аналіз підсумків обчислень дозволяє сформулювати наступні висновки:

• чим більший період усереднення, тим більш плавний характер здобуває лінія ковзної середньої;

• у міру збільшення інтервалу згладжування кількість елементів у ряді ковзних середніх скорочується (на два рівні при тричленному згладжуванні, на чотири рівні при чотирьох- і п'ятичленному вирівнюванні);

• значення ковзних середніх, розраховані по різних методиках, як правило, не збігаються.

Лабораторна робота № 14
«Перевірка наявності тенденції середнього рівня.
Згладжування емпіричних кривих (метод ковзної середньої)»

Згідно варіанту з табл. 14.1 записати постановку задачі.

Дослідити часовий ряд на наявність тренду (тенденції).

Провести вирівнювання за методом трьох- чотирьох- та п’ятичленної ковзної середньої.

Нанести вихідні дані на графік.

Всі варіанти мають часовий ряд (t). Для постановки задачі використати величину часового ряду згідно варіанту та верхню строчку таблиці 14.1.

Таблиця 14.1.

t (час)	Варіанти
Обєм реалізації тис. грн.	Прибуток фірми, тис. грн.	Витрати на рекла-му, грн.	Попит на продукцію ,т	Витрати на податки, тис. грн.	Попит на олію, тис. л	Попит на молоко, тис. л	Середній дохід на душу населення, тис. грн.	Собівартість 1 т продукцї, тис. грн.	Чисельність працюючих, чол.
y 1	y 2	y 3	y 4	y 5	y 6	y 7	y 8	y 9	y 10
		23,52		500,0	1109,1	29,244	16,9	3,9	5,6
	1053,1	34,1	1053,1	979,5	979,5	29,54	14,1	3,8
	1023,2	36,3	1023,2	896,8	896,8	25,58	14,8		5,6
	862,3	27,1	862,3	650,0	824,0	21,16	15,8	4,8	6,4
	804,9	25,2	804,9	723,1	723,1	18,04	15,8		6,8
	804,9		804,9	652,2	652,2		15,5	4,5	6,8
	559,5	14,3	559,5	578,3	856,0	17,16	12,5	4,2	6,8
	592,3	14,2	592,3	669,2	669,2	23,2	18,1	4,5	7,4
	583,1	11,5	583,1	755,6	755,6	27,18	19,1	4,6	6,6
	832,1	24,3	832,1	1026,3	1026,3	30,52	18,8		6,2
	851,7	21,5	851,7	605,0	811,0		16,4	4,8
	1395,1	44,5	1395,1	800,0	1094,5	29,94	18,1		6,8
	1086,3	34,1	1086,3	894,5	894,5	23,84	19,9	5,1	6,6
	802,1	28,2	802,1	780,8	780,8	20,92	17,3	5,4
	795,1	22,7	795,1	738,9	1000,0	19,26	19,5	5,4	8,4
	745,3	20,2	745,3	671,0	671,0				7,8
	676,3		676,3	559,7	559,7	15,48
	591,5	19,5	591,5	451,3	650,0	14,64
	411,4	19,9	411,4	354,6	354,6	12,68
	351,1	13,9	351,1	285,8	285,8	12,48
	301,3	10,1	301,3	219,4	219,4
	205,1	9,8	205,1	172,9	600,0
	151,9	9,7	151,9	319,4	319,4
	161,7	18,9	161,7
	644,5	35,2	644,5

Дата добавления: 2015-05-23