Перевірка наявності тенденції середнього рівня

Один із способів перевірки наявності тенденції заснований на порівнянні середніх рівнів ряду: часовий ряд розбивають на дві при­близно рівні частини, кожну з яких розглядають як деяку самостійну вибіркову сукупність, що має нормальний розподіл. Якщо часовий ряд має тенденцію до змінювання, то середні значення, обчислені для кожної сукупності, мають істотно (значно) різнитися між собою. Якщо розбіжність буде незначною (неістотною, випадковою), це оз­начатиме, що часовий ряд не має тенденції.

Отже, перевірка наявності тренда в досліджуваному ряді зводиться до перевірки гіпотези про рівність середніх двох нормально розподілених сукупностей.

Обчислення за цим методом складається з наступних етапів:

1) вхідний часовий ряд у₁,у₂, у₃, …, у_л розбивають на дві приблиз­но рівні частини обсягом п₁ ≈ п₂, де (п₁ + п₂ = п);

2) для кожної з частин обчислюють середні значення та дис­персії:

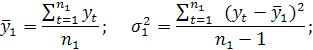
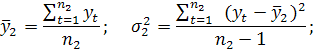
3) висувають основну гіпотезу про рівність середніх значень:

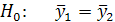проти альтернативної 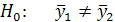і допоміжну гіпотезу
про рівність дисперсій 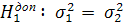проти альтернативної ;

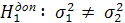4) перевіряють допоміжну гіпотезу за допомогою F-критерію Фішера. Для цього порівнюють розрахункове (експериментальне) зна­чення критерію:

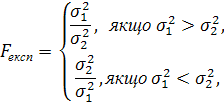
з табличним (критичним) значенням розподілу Фішера F_табл = F(а, k₁,k₂),
де a – заданий рівень значущості, k_i = п. –1 – степені вільності, і = 1,2.

Якщо за критерієм Фішера дисперсії виявляться нерівними
(F_експ > F_табл), то основну гіпотезу не перевіряють. Інакше переходять до наступного пункту;

5) основну гіпотезу про відсутність тренда перевіряють за допомогою
t-критерію Стьюдента. Для цього обчислюють вибіркову статис­тику – розрахункове значення критерію Стьюдента за формулою

де s – середньоквадратичне відхилення різниці середніх;

Якщо розрахункове значення t_експ менше від табличного значення розподілу Стьюдента (t_експ < t_табл), де t_табл =t(а, (п– 2)), то основна гіпоте­за Н₀приймається, тобто середні значення рівні, отже, ряд не має тренда.

Якщо H₀ відхиляється, то ряд має тенденцію до змінювання (тренд є).

Дата добавления: 2015-05-23