
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перевірка значущості та довірчі інтервали
|
|
|
|
Оцінка точності моделі
Визначаємо стандартні похибки оцінок параметрів моделі з урахуванням дисперсії залишків:
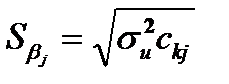 (13.6)
(13.6)
де 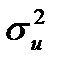 –дисперсія залишків:
–дисперсія залишків:
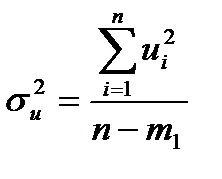 (13.7)
(13.7)
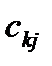 –елемент матриці похибок С (матриця, обернена до матриці коефіцієнтів системи нормальних рівнянь);
–елемент матриці похибок С (матриця, обернена до матриці коефіцієнтів системи нормальних рівнянь);
т1 – кількість параметрів моделі.
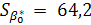
| < | 319,44 |
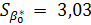
| < | 20,45 |
Порівняємо стандартні похибки оцінки з величиною оцінки: 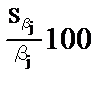 .
.
 319,44*100 = 20,1% 319,44*100 = 20,1%
|
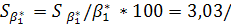 20,45*100 = 14,83% 20,45*100 = 14,83%
|
Визначається також середньоквадратичне відхилення (похибка)
 (13.8)
(13.8)
Відносна похибка
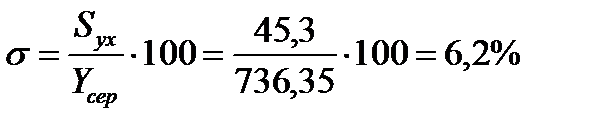 (13.9)
(13.9)
Перевірка значущості коефіцієнта детермінації
Для перевірки статистичної значущості коефіцієнта детермінації R2 висувається нульова гіпотеза
H0: R2=0.
H0: b1 = b2 =... = bn = 0.
Альтернативною до неї є
НА:bj ≠ 0
Для перевірки цих обчислюють експериментальне значення F-статистики:
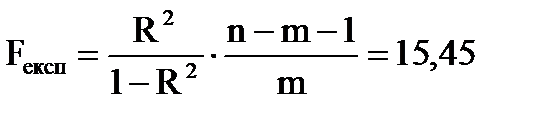 (13.10)
(13.10)
F0.05табл = 3,87
Fексп > F0.05табл
Нульова гіпотеза відхиляється, тобто існує такий коефіцієнт у регресійному рівнянні, який суттєво відрізняється від нуля, а відповідний фактор виливає на досліджувану змінну. Відхилення нуль-гіпотези свідчить про адекватність побудованої моделі.
Перевірка значущості коефіцієнта кореляції
Коефіцієнт кореляції перевіряється на значущість за допомогою t-критерію Ст’юдента. Фактичне значення t-статистики обчислюється за формулою
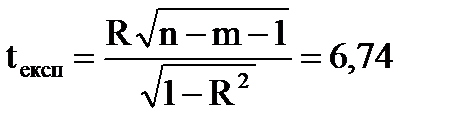 (13.11)
(13.11)
tтабл. = 2,45
|tексп|>tтабл,
Можна зробити висновок, що коефіцієнт кореляції достовірний (значущий), а зв'язок між залежною змінною та всіма незалежними факторами суттєвий.
Оцінка статистичної значущості параметрів моделі
Статистичну значущість кожного параметра моделі можна перевірити за допомогою t-критерію. При цьому нульова гіпотеза має вигляд
Н0 : bj = 0,
альтернативна
НА : bj ≠ 0.
Експериментальне значення t-статистики для кожного параметра моделі обчислюється за формулою
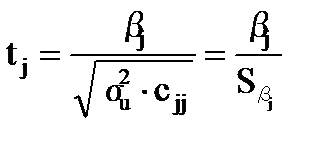
(13.12)
де Сjj – діагональний елемент матриці (Х′Х)–1;
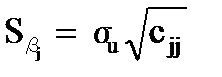
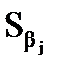 – стандартна похибка оцінки параметра моделі:
– стандартна похибка оцінки параметра моделі:
(13.13)
| t1 | t0 |
| 6,74 | 4,98 |
| tтабл = | 2,45 |
|tексп|>tтабл,
Значення t-статистики потрапляє до критичної області (за абсолютним значенням перевищує tтабл), приймається альтернативна гіпотеза про значущість параметрів.
Знайдемо інтервали надійності для кожного окремого параметра за формулою:

Оскільки оцінки параметрів моделі βj*, tспос і стандартні похибки параметрів моделі 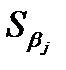 обчислені нами у попередніх пунктах, достатньо просто скористатися формулою для знаходження інтервалів:
обчислені нами у попередніх пунктах, достатньо просто скористатися формулою для знаходження інтервалів:
| = 319,44 - 2,4469 * 64,2 < b0 < 319,44 + 2,4469 * 64,2 |
| = 20,45 - 2,4469 * 3,03 < b1 < 20,45 + 2,4469 * 3,03 |
P (0162,34 < b0 < 476,54) = 0,95
P (13,03< b1 < 27,87) = 0,95
Розрахуємо коефіцієнт еластичності за формулою:
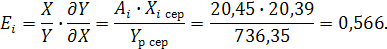
Коефіцієнт еластичності говорить про те, що збільшення витрат на впровадження інновацій на 1%, збільшить об’єм реалізації на 0,566%.
Зобразимо побудовану кореляційно-регресійну модель на графіку (рис.13.1 та рис. 13.2).
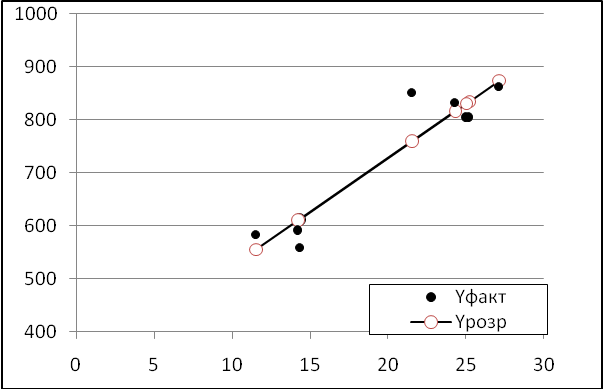
Рис. 13.1.
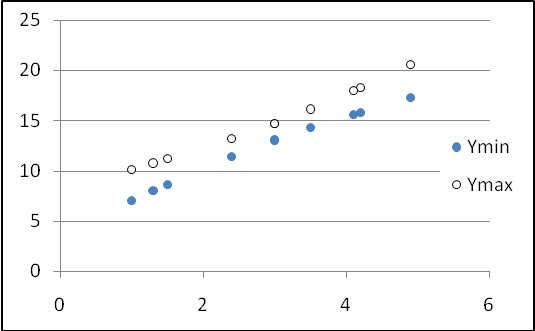
Рис. 13.2.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 1362; Нарушение авторских прав?; Мы поможем в написании вашей работы!