Приклад виконання лабораторної роботи

Задача. Маємо вибірку даних, які характеризують роботу підприємства за останні 8 місяців. Побудувати парну лінійну регресійну модель виду Y=b₀+b₁*X об’єму реалізації підприємства (Y), тис. грн., в залежності від витрат на впровадження інновацій в попередньому періоді (Х), тис грн.

Оцінити тісноту та значимість зв’язку між змінними моделі. Проаналізувати достовірність моделі та її параметрів.

Для аналізу необхідно розрахувати:

1) коефіцієнт детермінації;

2) скоригований коефіцієнт детермінації;

3) стандартні похибки оцінок параметрів моделі порівняти з величиною оцінок;

4) перевірити значущість змінної за t-критерієм Стьюдента;

5) знайти інтервали надійності для оцінок параметрів моделі;

6) відобразити модель на графіку;

7) знайти прогнозні значення матриці залежних змінних Y_пр,які відповідають очікуваним значенням матриці незалежних змінних X_пр.

8) зробити економічний висновок.

Вихідні дані для розрахунку в табл.13.3.

Таблиця 13.3

Спостереження	Об’єм реалізації, тис. грн.	Витрати на впровадження інновацій в попередньому періоді, тис. грн.
	Y	Х
	862,3	27,1
	804,9	25,2
	804,9	25,0
	559,5	14,3
	592,3	14,2
	583,1	11,5
	832,1	24,3
	851,7	21,5
Середнє значення	736,35

Для спрощення розрахунків використаємо вбудовану електронні в таблиці Microsoft Excel статистичну функцію ЛИНЕЙН. Ця функція застосовує метод найменших квадратів, щоб визначити оцінки параметрівлінійної регресії.

Суть методу найменших квадратів, полягає у наступному: сума квадратів відхилень ординат точки, що спостерігається, (X_i, Y_i) від відповідної ординати точки, що лежить на регресійній прямій, повинна бути найменшою

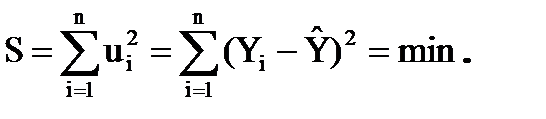
Результат застосування статистичної функції ЛИНЕЙН – це оцінка параметрів лінійної регресії та регресійна статистика:

20,45	319,44
3,033	64,203
0,883	48,935
45,47
108879,7	14367,5

b₀ = 319,44; b₁ = 20,45

Можна побудувати рівняння регресії: Y_розр = 319,44 + 20,45 Х.

Коефіцієнт регресії b₁ = 20,45 говорить про те, що збільшення витрат на впровадження інновацій на 1 тис. грн. збільшить об’єм реалізації на 20,45 тис. грн.

Для визначення статистичних коефіцієнтів та подальших розрахунків знаходимо відхилення (табл.13.4).

Таблиця 13.4

Yфакт	Yрозр	(Yфак -Yроз)^2	(Yфак -Yсер)^2	(Yроз -Yсер)^2
862,3	873,62		18842,0
804,9	834,76		9685,0
804,9	830,67		8896,7
559,5	611,86		15496,6
592,3	609,82		16009,9
583,1	554,61		33030,7
832,1	816,36		6401,3
851,7	759,10		517,6
		14367,5	108879,7	108879,7

Статистична функція ЛИНЕЙН обчислює до­даткову регресійну статистику:

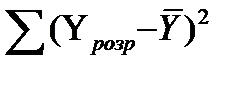– сума квадратів відхилення, що пояснюється регресією (колонка 5 з табл. 13.4);

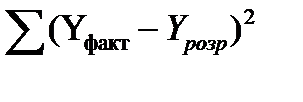– сума квадратів відхилення, що пояснюється похибкою u (колонка 3 з табл. 13.4);

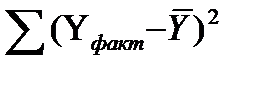– загальну суму квадратів відхилень розраховуємо (колонка 4 табл. 13.4).

Дата добавления: 2015-05-23