Тема 6. Кореляція двох змінних

Контрольні запитання

Приклад 5.

Таблиця 5.8

Значення показника G для різних k

Варіанти рішень (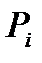)	Значення коефіцієнта k
0,00	0,25	0,50	0,75	1,00
P1	0,400	0,362	0,325	0,287	0,250
P2	0,750	0,612	0,475	0,337	0,200
P3	0,820	0,640	0,460	0,280	0,100
P4	0,800	0,650	0,500	0,350	0,200
Оптимальне рішення	P3	P4	P4	P4	P1

Із зміною коефіцієнта k змінюється варіант рішення, якому слід надати перевагу.

1. Сформулювати загальні принципи управління.

2. Як класифікуються функції управлінських рішень?

3. Назвіть види управлінських рішень.

4. Вимоги, що висуваються до управлінських рішень.

5. Методи та способи прийняття управлінських рішень.

6. Назвіть нестандартні підходи прийняття управлінських рішень.

7. Методи прийняття рішень в умовах неповної інформації та конфліктності.

8. Прийняття рішень в умовах відсутності повторюваності подій.

9. Назвіть способи зниження економічного ризику.

Література: [5, с. 346-372; 20, с. 5-10, 11-25, 46-61].

Економетрична модель – різновид економіко-математичної моделі, параметри якої оцінюються за допомогою методів математичної статистики.

Одним з основних підходів у вимірі зв'язку між досліджуваними показниками в економетричній моделі є кореляційно-регресивний аналіз. Він являє собою комплекс методів, за допомогою яких визначається вид рівняння для досліджуваних показників та розрахунок їх параметрів (регресивнийаналіз), а також встановлення тісноти та значимості зв'язку між змінними у рівнянні або рівняннях (кореляційний аналіз).

Варто відрізняти кореляційний зв'язок від функціонального. Для вивчення кореляційних зв'язків використовуються методи кореляційного і регресійного аналізу. Кореляційні методи застосовуються для опису взаємодії випадкових величин; методи регресійного аналізу – при дослідженні зв'язку між випадковими значеннями функції і невипадкових значень аргументів. Кореляційна залежність виявляє тенденцію у відношенні Y та Х.

Функціональний зв'язок – це такий зв'язок, при якому кожному значенню незалежної перемінної (аргументу) відповідає строго визначена величина залежної перемінної (функції). Функціональний зв'язок часто називають повним зв'язком, оскільки в ній відбивається вся безліч причинно-наслідкових відношень, що існують між розглянутими ознаками.

Y

X

Y – вартість;

Х – кількість одиниць.

Кореляційний зв'язок є неповним статистичним зв'язком. При кореляційній взаємодії на показник-функцію впливають не тільки фактори-аргументи, відібрані в процесі дослідження, але й безліч інших ознак, що не піддаються вивченню в силу недосконалості статистичного обліку, труднощі обчислення і т.п.

При кореляційному зв'язку кожному значенню незалежної перемінної можуть відповідати декілька значень (статистичний розподіл) функції.

Y

X

Y – продуктивність праці;

Х – втрати робочого часу.

Термінологія, яка використовується в економіко-математичному моделюванні

Система (у перекладі з грецької – ціле, зіставлене з частин) – це множина взаємозв’язаних елементів, які складають певну єдність.

Моделлю називається наближене чи спрощене відтворення найважливіших сторін, особливостей і характеристик систем, явищ і процесів, що вивчаються.

Економетричні (статистичні) моделі призначенні для аналізу і прогнозування розглядаємих економічних явищ в умовах невизначеності вхідних даних і реалізуються методами математичної статистики.

Економіко-математичні методи – узагальнена назва комплексу економіко-математичних підходів, об'єднаних для вивчення економіки та призначених для побудови, реалізації і дослідження економічних моделей.

Параметри – це чисельні ознаки показників, такі як норми витрат сировини, матеріалів, часу на виробництво тощо.

Регресія – це статистичний метод, який дозволяє знайти рівняння, що найкращим чином описує масив фактичних даних (спостережень).

В усіх випадках необхідно, щоб модель мала достатньо детальний опис об'єкту, який дозволяв би здійснювати вимір економічних величин та їх взаємозв'язок, щоб були виділені фактори, які впливають на досліджувані показники.

Зміст змінних і рівнянь в економетричній моделі

В регресійному аналізі розрізняють рівняння парної (простої) та множинної (багатофакторної) регресії.

Коли зв'язок із залежною змінною Y здійснюється з одним видом незалежних змінних X, то рівняння регресії є найпростішим і має назву рівняння парної регресії (проста модель). Якщо залежна змінна у пов'язана з декількома видами незалежних змінних X_j (j=1...т), то така залежність має назву рівняння множинної регресії.

У загальному вигляді проста вибіркова регресійна модель запишеться так:

Y = f (X) + u,

де x – незалежна змінна,

Y – залежна змінна,

u – випадкова складова.

Незалежні фактичні змінні х найчастіше бувають детермінованими і вони є наперед заданими змінними, або вхідними показниками.

Випадкові складові и називають ще стохастичними складовими,помилками або частіше залишками. Вони є наслідками помилок спостережень, містять у собі вплив усіх випадкових факторів, а також факторів, які не входять у модель.

Прості лінійні регресійні моделі встановлюють лінійну залежність між двома змінними. При цьому одна із змінних вважається залежною змінною (Y)та розглядається як функція від незалежної змінної (X).

У загальному вигляді проста вибіркова регресійна модель запишеться так:

Y = a₀ + a₁ X + u,

де Y – вектор спостережень за залежною змінною;

X – вектор спостережень за незалежною змінною;

a₀, a₁ – невідомі параметри регресійної моделі;

u – вектор випадкових величин (помилок).

У загальному матричному вигляді економетрична модель записується так:

Y=AX+u,

де А – матриця параметрів моделі розміром m×n (m – кількість незалежних змінних, n – число спостережень);

Y – матриця значень залежної змінної;

Х – матриця незалежних змінних;

u – матриця випадкової складової.

Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Отже, модель (2.1) є лінійною регресійною моделлю.

Французький математик Лежандром у XIX ст. запропонував метод знаходження теоретичної лінії, наближеної до фактичних даних як мінімальну суму (S) квадратів відхилення їх ординат Y_iвід теоретичних значень Y:

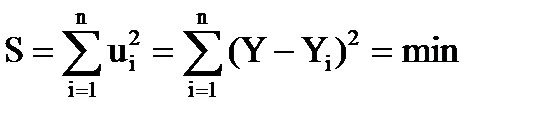
Назва цього методу – метод найменших квадратів (або скорочено 1МНК).

Лабораторна робота № 13
«Модель парної лінійної кореляційної залежності»

Задача. Згідно з вибіркою статистичних даних (табл. 13.2) потрібно побудувати лінійну модель вигляду Y=b₀+b₁·X залежності об’єму реалізації продукції від витрат на впровадження інновацій в попередньому періоді.

Потрібно: оцінити точність і достовірність моделі; побудувати модель в декартових координатах; виконати економічний аналіз отриманих результатів.

Вибірка даних характеризує роботу підприємства за останні 10 місяців. У вибірці кожному значенню Y – об’єм реалізації (тис. грн.) відповідає значення X – витрати на впровадження інновацій в попередньому періоді (тис грн.).

Номер варіанту завдання з табл. 13.2 визначається за варіантом з табл.13.1. Перша цифра – номер стовпця для показника Y, а друга – номер стовпця для показника X.

Таблиця 13.1

Варіант	Номери варіантів за завданням		Варіант	Номери варіантів за завданням		Варіант	Номери варіантів за завданням
	1, 12			1, 11			1, 19
	2, 20			2, 12			2, 13
	3, 14			3, 13			3, 15
	4, 11			4, 14			4, 19
	5, 14			5, 20			5, 19
	6, 16			6, 17			6, 14
	7, 15			7, 17			7, 13
	8, 15			8, 18			8, 12
	9, 13			9, 19			9, 11
	10, 12			10, 20			10, 19

Таблиця 13.2

Вихідні дані для виконання лабораторних робіт

Номер	Варіанти
спосте­реження
	151,9	411,4	676,3	804,9	559,5	804,9	851,7	745,3	583,1	802,1
	161,7	559,5	745,3	832,1	583,1	559,5	1395,1	676,3	591,5	804,9
	205,1	583,1	795,1	851,7	592,3	592,3	1086,3	591,5	592,3	804,9
	301,3	591,5	802,1	862,3	704,9	583,1	802,1	411,4	676,3	832,1
	351,1	592,3	804,9	1023,2	804,9	832,1	795,1	351,1	745,3	851,7
	411,4	676,3	804,9	1053,1	832,1	851,7	745,3	301,3	795,1	862,3
	559,5	745,3	832,1	1086,3	951,7	1395,1	676,3	205,1	802,1	1023,2
	583,1	795,1	851,7		962,3	1086,3	591,5	151,9	804,9	1053,1
	591,5	802,1	862,3		1023,2	802,1	411,4	161,7	804,9	1086,3
	592,3	804,9	1023,2	1395,1	1053,1	795,1	351,1		832,1

Продовження таблиці 13.2

Номер	Варіанти
спосте­реження
	3,52	11,5	19,5	24,3	11,5		21,5	20,2		21,5
	8,9	13,9	19,9		14,2	14,3	44,5		14,2	22,7
	9,7		20,2	25,2	14,3	14,2	34,1	19,5	14,3	24,3
	9,8	14,2	21,5	27,1	21,5	11,5	28,2	19,9	19,5
	10,1	14,3	22,7	28,2	24,3	24,3	22,7	13,9	19,9	25,2
	11,5	19,5	24,3	34,1		21,5	20,2	10,1	20,2	27,1
	13,9	19,9		34,1	25,2	44,5		9,8	21,5	28,2
		20,2	25,2	35,2	27,1	34,1	19,5	9,7	22,7	34,1
	14,2	21,5	27,1	36,3		28,2	19,9	8,9	24,3	34,1
	14,3	22,7	28,2	44,5	34,1	22,7	13,9	35,2		35,2

Дата добавления: 2015-05-23