Короткі теоретичні відомості. Теорема.Якщо додатне наближене число а має п точних десяткових знаків, то відносна похибка δ цього числа задовольняє умову

Теорема. Якщо додатне наближене число а має п точних десяткових знаків, то відносна похибка δ цього числа задовольняє умову

δ ≤ ,

де а_т – перша значуща цифра числа а.

Доведення. Нехай а = α_m · 10 ^m + α_{m - 1} · 10^{m - 1} +... + α_{m – n +1} · 10^{m – n + 1}

є наближеним значенням точного числа А з n точними знаками. Тоді, згідно з означенням числа точних знаків наближеного числа, одержуємо

∆ = | А – а |≤ · 10^{m – n + 1}.

Звідси

- · 10^{m – n + 1} ≤ А – а ≤ · 10^{m – n + 1}.

Тому

А ≥ а - · 10^{m – n + 1} ≥ α_m · 10 ^m - · 10^{m – n + 1}

або

А ≥ · 10^{m .}

Права частина отриманої нерівності досягає найменшого значення при п = 1, тому

А ≥ · 10^m ≥ · 10^m (2 а _m - 1).

Оскільки 2 а _m - 1 = а_т + (а_т – 1) ≥ а _m , то

А ≥ а _m · 10^m.

Тепер, згідно з означенням,

δ = ,

або

δ ≤ .

Наслідок 1. За граничну відносну похибку наближеного додатного числа а з п точними десятковими знаками можна прийняти

δ _a =

де а _m - перша значуща цифра числа а.

Наслідок 2. За граничну відносну похибку наближеного додатного числа а з п точними десятковими знаками при п ≥ 2 практично можна прийняти

δ _a = .

Справді, якщо п>2, то числом у нерівності можна знехтувати. Тоді

А ≥ · 10^m · 2 а _m = а _m · 10^m.

Тому

δ = ,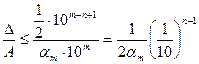

Приклад 1. Яка гранична відносна похибка наближеного числa а= 3,14, що замінює точне число А = π?

Оскільки п = 3 і а_т = 3, то на підставі наслідку 2

δ _a = %.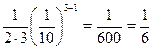

Приклад 2. Зі скількома точними десятковими знаками треба взяти , щоб відносна похибка була не більша за 0,1%?

Оскільки а_т = 4, δ ≤ 0,001, то на підставі наслідку 1 має викону­ватися нерівність:

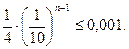
Звідси 10^{n – 1} ≥ 250 або п ≥ 4.

Для визначення кількості точних знаків наближеного числа а, якщо відома його відносна похибка δ, можемо скористатися наближеною формулою

δ =

де ∆ - абсолютна похибка наближеного числа а. Із цієї формули одержуємо, що ∆ = δ| a |.Маючи ∆, на підставі означення легко знайти кількість точних десяткових знаків наближеного числа а.

Приклад 3. Число а = 7654 має відносну похибку δ = 0,01. Скільки в ньому точних цифр?

Оскільки

∆ = δ a = 76,54 < · 10³

то число а має лише одну точну цифру.

Дата добавления: 2015-05-23