Применение термодинамических потенциалов для описания эффекта Джоуля-Томсона 1 страница

Адиабатическое расширение газа обычно приводит к изменению его температуры. Если при адиабатическом расширении уменьшение внутренней энергии газа равно совершенной им механической работе над внешними телами, то такой процесс будет обратимым. При обратимом адиабатическом расширении температура газа изменяется в соответствии с уравнением адиабаты. Для идеального газа эта зависимость имеет вид (см. формулу (2.86)):

,

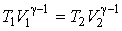(4.54)

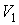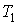где: и - объем и температура газа в начале процесса, 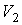и 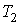- объем и температура газа после расширения. Так как 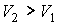, то из формулы (4.54) следует, что при обратимом адиабатическом расширении идеального газа происходит уменьшение его температуры: .

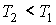Указанное уменьшение температуры идеального газа при его адиабатическом расширении происходит только в том случае, если этот процесс является обратимым. Описанный в параграфе 2.4 опыт Гей-Люссака показал, что при необратимом адиабатическом расширении идеального газа без совершения им работы над внешними телами его внутренняя энергия и температура остаются неизменными. Поэтому при таком расширении использование выражения (4.54) для определения температуры идеального газа становится невозможным.

При необратимом адиабатическом расширении величина и знак изменения температуры зависят от свойств использующегося в процессе газа. Необратимое адиабатическое расширение газа может быть осуществлено путем его пропускания через пористую перегородку, которая обеспечивает медленное течение газа без возникновения в нем турбулентных потоков, что позволяет считать кинетическую энергию газа малой величиной. Наблюдаемый при этом эффект, заключающийся в изменении температуры газа, называется эффектом Джоуля-Томсона. На примере описания этого эффекта рассмотрим применение метода термодинамических потенциалов.

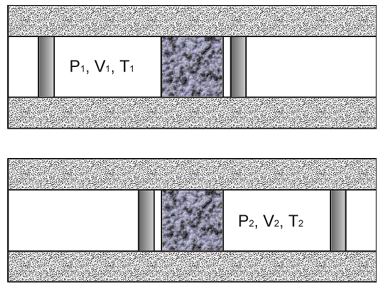
На рис. 4.1 схематически изображен опыт Джоуля-Томсона. Внутри теплоизолированной трубки помешалась пористая перегородка, через которую осуществлялось медленное стационарное течение газа. Газ внутри пористой перегородки находится в неравновесном состоянии, а процесс его протекания - является необратимым. Но вследствие медленности течения, газ по обе стороны от перегородки можно считать находящимся в равновесии. Давления 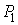и 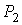в обеих частях цилиндрической трубки поддерживались постоянными. Пусть при протекании через пористую перегородку некоторой порции газа, имевшей объем 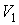и температуру 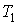, она приобрела объем 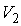и температуру 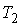(см. рис. 4.1).

Рис. 4.1. Схема опыта Джоуля-Томсона

Проведем описание процесса протекания газа через пористую перегородку. Считая этот процесс достаточно медленным и адиабатическим, а также, учитывая постоянство давлени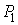й и 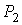, применим первое начало термодинамики:

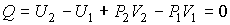
(4.55)

или учитывая определение энтальпии (4.28)

.

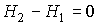(4.56)

Следовательно, рассматриваемый процесс является не только адиабатическим, но и изоэнтальпийным.

Далее будем считать, что изменения давления 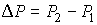и температуры 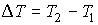газа в рассматриваемом процессе малы. Тогда с точностью до величин второго порядка малости можно записать:

.

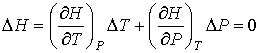(4.57)

Следовательно:

.

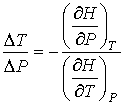(4.58)

Для определения частных производных энтальпии 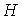найдем полный дифференциал от выражения (4.28)

.

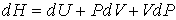(4.59)

Тогда с учетом формулы (4.57) имеем:

.

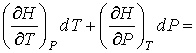
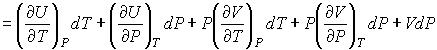(4.60)

Из формулы (4.60) следует:

,

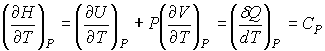(4.61)

.

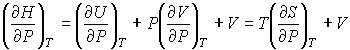(4.62)

где - теплоемкость газа при постоянном давлении. При получении выражения (4.61) использована формула (1.5) с учетом выражения (1.12), а при получении формулы (4.62) - уравнение (4.24).

Дифференцирование выражения (4.43) по давлению 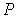, а формулы (4.44) по температуре 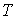, с учетом равенства перекрестных производных потенциала Гиббса

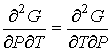
(4.63)

дает

.

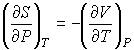(4.64)

Подстановка выражения (4.64) в формулу (4.62) и далее, с ее учетом, формул (4.61) и (4.62), в выражение (4.58) позволяет получить следующее соотношение:

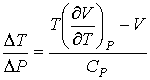
(4.65)

или для бесконечно малого изменения давления

,

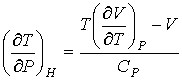(4.66)

где производная 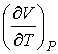определяется уравнением состояния газа. Формула (4.65) позволяет рассчитать изменение температуры газа при просачивании его через пористую перегородку.

Если при проведении опыта использовать идеальный газ, описываемый уравнением Клапейрона-Менделеева (2.10), то имеем:

.

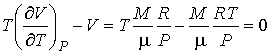(4.67)

Следовательно, для идеального газа 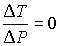и изменения его температуры при прохождении через пористую перегородку не происходит.

Таким образом, при необратимом адиабатическом расширении идеального газа через пористую перегородку его температура не изменяется, в отличие от обратимого адиабатического расширения, приводящего в соответствии с формулой (4.54) к охлаждению идеального газа.

Данный результат связан с тем, что при адиабатическом расширении идеального газа в опыте Джоуля-Томсона механическая работа не совершается, в отличие от обратимого адиабатического расширения. При применении в этом опыте реального газа совершаемая им механическая работа определяется силами межмолекулярного взаимодействия, и её знак зависит от этих сил.

Рассмотрим применение в опыте Джоуля-Томсона газа Ван-дер-Ваальса, уравнение (2.117) для одного моля которого имеет вид:

.

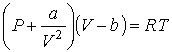(4.68)

Раскроем скобки в этом уравнении

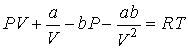
(4.69)

и пренебрегая третьим и четвертым слагаемыми в левой части получившегося выражения в связи с их малостью (считая 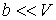), продифференцируем его по температуре 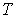при постоянном давлении :

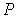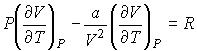
(4.70)

или

.

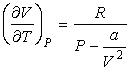(4.71)

Выражая 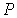из формулы (4.68) и подставляя в (4.71) с последующим пренебрежением малыми слагаемыми имеем:

.

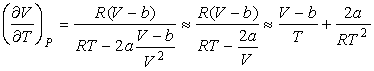(4.72)

Тогда формула (4.65) для отношения 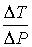принимает вид

.

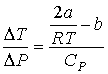(4.73)

Из этой формулы следует, что существует температура 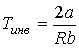, при которой газ Ван-дер-Ваальса, проходя через пористую перегородку, не изменяет свою температуру. Эта температура 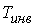называется температурой инверсии, так как при 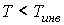отношение 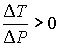и наблюдается охлаждение газа (так как 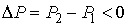и, следовательно 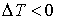), а при 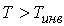отношение 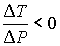и газ нагревается. В первом случае эффект Джоуля-Томсона считается положительным, а во втором - соответственно отрицательным.

Как следует из проведенного анализа, при выполнении условия 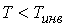наблюдается охлаждение газа при необратимом адиабатическом расширении. По этой причине, как уже отмечалось в параграфе 2.7, эффект Джоуля-Томсона применяется для охлаждения и ожижения газов, таких, например, как водород и гелий.

Процесс охлаждения газа может быть реализован так же с помощью обратимого адиабатического расширения. При таком расширении процесс будет происходить при постоянной энтропии, то есть этот процесс будет изоэнтропийным. Тогда для обратимого адиабатического расширения газа можно на основании формулы (4.29) записать:

.

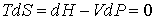(4.74)

С учетом формулы (4.57) имеем

.

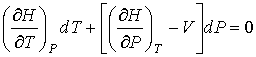(4.75)

Отсюда следует, что при описании обратимого адиабатического процесса вместо формулы (4.58) необходимо использовать выражение

.

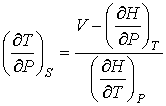(4.76)

С учетом полученных выше выражений (4.61), (4.62) и (4.64) вместо формулы (4.66) можно записать:

.

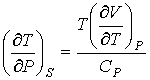(4.77)

Для газов характерно изобарическое расширение при их нагревании. Поэтому из условия

,

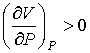(4.78)

справедливого для всех газов, следует, что

.

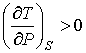(4.79)

Поэтому при обратимом адиабатическом расширении газ охлаждается (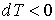), так как при этом его давление уменьшается (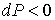). В частности, при расширении идеального газа, из формул (4.67) и (4.77) имеем:

.

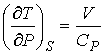(4.80)

Для газа Ван-дер-Ваальса при обратимом адиабатическом расширении с учетом формулы (4.72) при условии 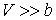получим следующее выражение для определения изменения его температуры

.

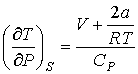(4.81)

Из выражений (4.80) и (4.81) следует, что как идеальный газ, так и газ Ван-дер-Ваальса охлаждается при обратимом адиабатическом расширении.

Таким образом, применение для охлаждения газа обратимого адиабатического процесса имеет принципиальное преимущество по сравнению с применением эффекта Джоуля-Томсона, связанное с отсутствием явления инверсии. Однако для реализации этого преимущества возникает необходимость создания технических устройств, в которых газ должен совершать механическую работу над внешними телами, например, над поршнем или турбиной. Только в этом случае расширение газа может быть обратимым. Машины, служащие для получения низких температур за счет расширения газа с совершением им механической работы, получили названия детандеров. Для охлаждения больших количеств газа наибольшее распространение получили турбодетандеры, в которых вместо поршня используется турбина. Обеспечение работоспособности детандеров и турбодетандеров в условиях низких температур является достаточно сложной технической задачей.

Задача 4.5. Фотонный газ, имеющий температуру 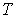, находится в объеме 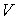. Величину этого объема резко увеличивают на 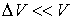, совершая необратимый адиабатический процесс. Считая, что фотонный газ не совершает при рассматриваемом процессе работы, определить изменение его температуры 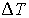. Решить задачу для случая обратимого адиабатического расширения фотонного газа. Использовать выражения для внутренней энергии 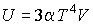и энтропии 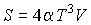фотонного газа.

Решение: Так как рассматриваемый необратимый адиабатический процесс происходит без теплообмена с окружающей средой: 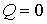, и, в соответствии с условием задачи, считается, что при его протекании работа не совершается: 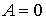, то из первого начала термодинамики следует сохранение внутренней энергии фотонного газа: 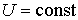. Тогда имеем:

.

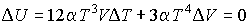Отсюда следует:

.

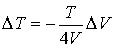В случае обратимого адиабатического процесса должна сохранятся энтропия фотонного газа: 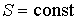. Поэтому

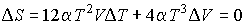
или

.

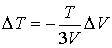Как следует из полученных результатов, охлаждение фотонного газа зависит от того, какой адиабатический процесс (обратимый или необратимый) над ним осуществляется. При этом обратимое адиабатическое расширение фотонного газа обеспечивает его более интенсивное охлаждение, чем необратимое.

4Вязкость, идеальный газ. Сжимаемость.

Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: пуаз, 0,1Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести.

Вязкость — важная физико-химическая характеристика веществ. Значение Вязкость приходится учитывать при перекачивании жидкостей и газов по трубам (нефтепроводы, газопроводы). Вязкость расплавленных шлаков весьма существенна в доменном и мартеновском процессах. Вязкость расплавленного стекла определяет процесс его выработки. По Вязкость во многих случаях судят о готовности или качестве продуктов или полупродуктов производства, поскольку Вязкость тесно связана со структурой вещества и отражает те физико-химические изменения материала, которые происходят во время технологических процессов. Вязкость масел имеет большое значение для расчёта смазки машин и механизмов и т.д.

Молекулярно-кинетическая теория объясняет Вязкость движением и взаимодействием молекул. В газах расстояния между молекулами существенно больше радиуса действия молекулярных сил, поэтому Вязкость газов определяется главным образом молекулярным движением. Между движущимися относительно друг друга слоями газа происходит постоянный обмен молекулами, обусловленный их непрерывным хаотическим (тепловым) движением. Переход молекул из одного слоя в соседний, движущийся с иной скоростью, приводит к переносу от слоя к слою определённого количества движения. В результате медленные слои ускоряются, а более быстрые замедляются. Работа внешней силы F, уравновешивающей вязкое сопротивление и поддерживающей установившееся течение, полностью переходит в теплоту.

Вязкость газа не зависит от его плотности (давления), так как при сжатии газа общее количество молекул, переходящих из слоя в слой, увеличивается, но зато каждая молекула менее глубоко проникает в соседний слой и переносит меньшее количество движения (закон Максвелла). Для Вязкость идеальных газов в молекулярно-кинетической теории даётся следующее соотношение:

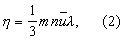
где m — масса молекулы, n — число молекул в единице объёма, 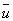— средняя скорость молекул и l — длина свободного пробега молекулы между двумя соударениями её с другими молекулами. Так как 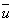возрастает с повышением температуры Т (несколько возрастает также и l), то Вязкость газов увеличивается при нагревании (пропорционально 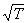). Для очень разреженных газов понятие Вязкость теряет смысл.

В жидкостях, где расстояния между молекулами много меньше, чем в газах, Вязкость обусловлена в первую очередь межмолекулярным взаимодействием, ограничивающим подвижность молекул. В жидкости молекула может проникнуть в соседний слой лишь при образовании в нём полости, достаточной для перескакивания туда молекулы. На образование полости (на «рыхление» жидкости) расходуется так называемая энергия активации вязкого течения. Энергия активации уменьшается с ростом температуры и понижением давления. В этом состоит одна из причин резкого снижения Вязкость жидкостей с повышением температуры (рис. 3) и роста её при высоких давлениях. При повышении давления до нескольких тыс. атмосфер h увеличивается в десятки и сотни раз. Строгая теория Вязкость жидкостей, в связи с недостаточной разработанностью теории жидкого состояния, ещё не создана. На практике широко применяют ряд эмпирических и полуэмпирических формул Вязкость, достаточно хорошо отражающих зависимость Вязкость отдельных классов жидкостей и растворов от температуры, давления и химического состава.

Вязкость жидкостей зависит от химической структуры их молекул. В рядах сходных химических соединений (насыщенные углеводороды, спирты, органические кислоты и т.д.) Вязкость изменяется закономерно — возрастает с возрастанием молекулярной массы. Высокая Вязкость смазочных масел объясняется наличием в их молекулах циклов (см. Циклические соединения, Нафтены). Две жидкости различной Вязкость, которые не реагируют друг с другом при смешивании, обладают в смеси средним значением Вязкость Если же при смешивании образуется химическое соединение, то Вязкость смеси может быть в десятки раз больше, чем Вязкость исходных жидкостей. На этом основано применение измерений Вязкость в качестве метода физико-химического анализа.

Возникновение в жидкостях (дисперсных системах или растворах полимеров) пространственных структур, образуемых сцеплением частиц или макромолекул, вызывает резкое повышение Вязкость При течении «структурированной» жидкости работа внешней силы затрачивается не только на преодоление истинной (ньютоновской) Вязкость, но и на разрушение структуры (см. Реология).

Для нормальных вязких жидкостей между количеством жидкости Q, протекающей в единицу времени через капилляр, и давлением p существует прямая пропорциональность (см. Пуазёйля закон). Течение структурированных жидкостей не подчиняется этому закону, для них кривые зависимости Q от р выпуклы к оси давления (рис. 4), что объясняется непостоянством h. Аномальной Вязкость, характерной для структурированных жидких систем, обладают важнейшие биологические среды — цитоплазма и кровь.

М. П. Воларович.

Вязкость биологических сред определяется в большинстве случаев структурной вязкостью. Вязкость жидкого содержимого клетки-цитоплазмы связана со структурой составляющих её биополимеров и субклеточных образований, что вызывает отклонения (характера тиксотропии) вязкого течения от ньютоновского закона нормальных жидкостей. Методы измерения Вязкость биологических сред — наблюдение скорости перемещения гранул при центрифугировании или железных опилок в магнитном поле, измерение среднего смещения броуновских частиц (см. Броуновское движение). Абсолютная вязкость цитоплазмы колеблется от 2 до 50 спз (1 спз = 10^-3 н · сек/м ²), она меняется в различных частях клетки и в разные периоды клеточного цикла. С понижением температуры ниже 12—15°С и при повышении её свыше 40—50°С вязкость цитоплазмы увеличивается. При воздействии облучения наблюдается сначала уменьшение вязкости, а затем, при увеличении дозы, — её возрастание.

Вязкость ликвора, лимфы и плазмы крови достаточно точно описывается ньютоновским законом вязкого течения, она исследуется в капиллярных или цилиндрических вискозиметрах. Кровь — неньютоновская жидкость, так как содержит структурированные компоненты — белки и клетки крови, её вязкость у человека в норме 4—5 спз, при патологии колеблется от 1,7 до 22,9 спз, что отражается в реакции оседания эритроцитов (РОЭ).

Лит.: Гaтчек Э., Вязкость жидкостей, пер. с англ., 2 изд., М. — Л., 1935; Труды совещания по вязкости жидкостей и коллоидных растворов, т. 1—3, М. — Л., 1941—45; Френкель Я. И., Кинетическая теория жидкостей, М. — Л., 1945; Фукс Г. И., Вязкость и пластичность нефтепродуктов, М., 1956; Голубев И. Ф., Вязкость газов и газовых смесей, М., 1959; Справочник химика, 2 изд., т. 1, Л. — М.,1963; Руководство по цитологии, т. 1—2, М. — Л., 1965—66; Heilbrunn L. V. The viscosity of protoplasm, W., 1958.

Н. Н. Фирсов.

Рис. 4. Зависимость количества жидкости Q, протекающей через капилляр в 1 сек, от давления p для нормальных (ньютоновских) и аномальных (неньютоновских) жидкостей.

Рис. 2. Вязкость некоторых расплавленных металлов в спз.

S, из которых нижняя (А) неподвижна, а верхняя (В) под действием тангенциальной силы F движется с постоянной скоростью v0; v(z) — зависимость скорости слоя от его расстояния z от неподвижной пластинки; Dx0 — величина начального сдвига жидкости." href="a_pictures/18/10/212574081.jpg"> S, из которых нижняя (А) неподвижна, а верхняя (В) под действием тангенциальной силы F движется с постоянной скоростью v0; v(z) — зависимость скорости слоя от его расстояния z от неподвижной пластинки; Dx0 — величина начального сдвига жидкости." title="Рис. 1. Схема однородного сдвига (вязкого течения) слоя жидкости, заключенного между двумя твердыми пластинками площадью S, из которых нижняя (А) неподвижна, а верхняя (В) под действием тангенциальной силы F движется с постоянной скоростью v0; v(z) — зависимость скорости слоя от его расстояния z от неподвижной пластинки; Dx0 — величина начального сдвига жидкости." src="a_pictures/18/10/th_212574081.jpg">
Рис. 1. Схема однородного сдвига (вязкого течения) слоя жидкости, заключенного между двумя твердыми пластинками площадью S, из которых нижняя (А) неподвижна, а верхняя (В) под действием тангенциальной силы F движется с постоянной скоростью v0; v(z) — зависимость скорости слоя от его расстояния z от неподвижной пластинки; Dx0 — величина начального сдвига жидкости.

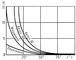
Рис. 3. Измерение вязкости некоторых смазочных масел в зависимости от температуры (h дана в пз).

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Дата добавления: 2015-05-23