Уравнения Лагранжа второго рода

В этом разделе мы выведем уравнения движения механических систем с односторонними связями в форме уравнений Лагранжа второго рода. Такие уравнения можно получить, обычным образом, если удерживающие и односторонние связи голономны. Пусть 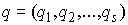обобщенные координаты тогда

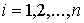, (10.1)

Мы считаем, что функции 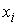имеют, по крайней мере, второй класс гладкости. Тогда траектория движения – это абсолютно непрерывная вектор-функция, производная которой является функцией ограниченной вариации. Односторонние связи в обобщенных координатах задаются системой неравенств 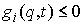, . Из (10.1) получаем

(10.2)

отсюда

(10.3)

Кроме того

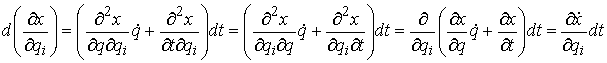
или, в матричной форме

(10.4)

Подставив (10.2) в уравнения удерживающих связей (7.3) получим систему 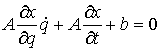, которая должна тождественно выполняться при всех . Отсюда

(10.5)

Воспользуемся матричной формой уравнений Лагранжа 1-го рода (8.11). 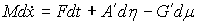(10.6)

Где 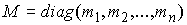– диагональная матрица, с элементами на диагонали, 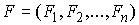– сводный вектор сил, 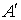– транспонированная матрица 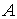из (7.3), 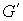– транспонированная матрица Якоби 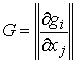. Домножив обе части (10.6) слева на матрицу 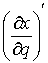получим

Матрица 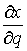абсолютно непрерывна поэтому, используя формулу Лейбница (4.1) получаем на действительной траектории

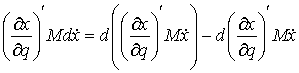
Использовав (10.3, 10.4), получаем отсюда

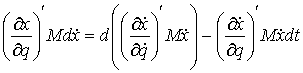
Введем кинетическую энергию системы . Тогда

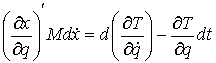(10.8)

Как обычно, обозначим

(10.9)

вектор обобщенных сил , , 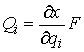. Далее, в силу (10.5) имеем

(10.10)

Обозначим 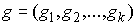тогда и

(10.11)

Подставив (10.8-10.11) в (10.6) получим

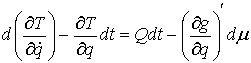(10.12)

или, в покоординатном виде

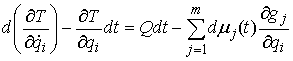(10.13)

Теорема Аппеля. Пусть в момент 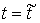траектория движения находится на границе односторонних ограничений, и скорость претерпевает скачок. Тогда вектор обобщенных импульсов 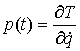также имеет скачок. Обозначим , (для функции ограниченной вариации эти величины всегда существуют). Тогда из (10.13) имеем

(10.14)

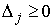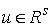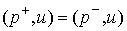Где – некие неотрицательные величины. Возьмем любой вектор , касающийся границы односторонних ограничений в точке . Тогда из (10.14) имеем . Т.е. сохраняются проекции вектора обобщенного импульса на плоскость касательную поверхности удара. Обычно это утверждение формулируется для случая, когда в окрестности точки односторонние связи имеют простейший вид: , . Тогда сохраняются обобщенные импульсы ,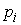

,

Потенциальный случай. Если силы потенциальны и имеют силовую функцию , то введем, как обычно, функцию Лагранжа . И уравнения движения приобретут форму

(10.15)

Здесь везде 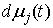– неотрицательные меры Лебега-Стилтьеса, каждая из которых сосредоточена на множестве моментов времени, в которые траектория движения выходит на границу соответствующего одностороннего ограничения .

Дата добавления: 2015-05-23