
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гидравлический удар в трубах
|
|
|
|

Если внезапно остановить движущийся в трубе поток жидкости, то в соответствии с уравнением (3.1) изменение количества движения вызовет возникновение избыточной силы давления жидкости на задвижку (рис. 7.18). Очевидно, что абсолютно несжимаемая жидкость вызвала бы бесконечное по величине давление при мгновенной остановке в недеформируемом трубопроводе. Однако в результате сжимаемости реальных жидкостей остановка жидкости в трубе даже при мгновенном закрытии заслонки происходит во времени, и волна давления распространяется в среде со скоростью, равной скорости звука с. Таким образом, остановка жидкости на участке длиной х произойдет за время t=x/c, при этом количество движения  изменится линейно от начального
изменится линейно от начального 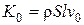 до 0, т.е.
до 0, т.е.
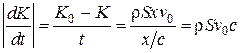 (7.26)
(7.26)
где  — средняя скорость течения жидкости в трубе до остановки; s — площадь сечения трубопровода.
— средняя скорость течения жидкости в трубе до остановки; s — площадь сечения трубопровода.
В результате изменения количества движения возникнет
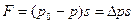 (7.27)
(7.27)
Приравняв (7.26) и (7.27), получим выражение для расчета скачка давления 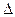 р, возникающего при гидравлическом ударе:
р, возникающего при гидравлическом ударе:
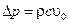 (7.28)
(7.28)
После остановки жидкости во всем объеме трубы начинается процесс послойного расширения. Слева направо идет волна разрежения. Итак, перед заслонкой давление р0 сохраняется в течение времени Т=2l/с. Величина Т называется фазой прямого удара. Более детальный анализ гидравлического удара проведем на основании уравнения движения (5.1) и уравнения неразрывности (2.12) идеальной сжимаемой жидкости. Анализ проведем в предположении, что в уравнении динамики можно не учитывать сжимаемость, т. е. считаем относительное изменение плотности жидкости незначительным. В этом случае при течении вдоль оси х в каналах постоянного сечения конвективное ускорение равно 0, т. е.
 уравнение (5.1) в проекции на ось х примет с учетом того, что X=0, вид
уравнение (5.1) в проекции на ось х примет с учетом того, что X=0, вид
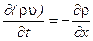 (7.29)
(7.29)
(дополнительно принять, что ux= 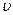 ).
).
Уравнение (2.12) для одномерной задачи можно записать так
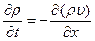 (7.30)
(7.30)
Если плотность жидкости 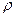 однозначно определяется давлением (такие жидкости называются баротропными), т. е.
однозначно определяется давлением (такие жидкости называются баротропными), т. е. 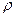 =
= 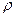 (р), то в (7.30)
(р), то в (7.30)  Производная d
Производная d 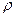 /dp всегда больше нуля и постоянна. Обозначим dp/d
/dp всегда больше нуля и постоянна. Обозначим dp/d 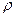 =c2. С учетом этого уравнение (7.30) примет вид
=c2. С учетом этого уравнение (7.30) примет вид
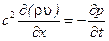 (7.31)
(7.31)
(для газов p/ 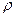 =nRT; при T=const dp/d
=nRT; при T=const dp/d 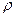 =RTn=const).
=RTn=const).
Решим совместно уравнения (7.29) и (7.31). Продифференцировав (7.29) по t, (7.31) по х и приравняв смешанные вторые производные, найдем
 (7.32)
(7.32)
По аналогии, взяв соответственно производные по х и t, получим
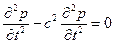 (7.33)
(7.33)
Уравнения (7.32) и (7.33) называются в математике волновыми. Они могут быть проинтегрированы в общем виде введением новых переменных
 и
и 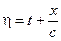 (7.34)
(7.34)
Решения имеют вид
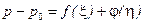 (7.35)
(7.35)
 (7.36)
(7.36)
В случае закрытия трубопровода в начальный период имеет место одна волна и решение (7.35) и (7.36) с учетом (7.34) следует искать в виде
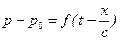 (7.37)
(7.37)
Из (7.37) видно, что р — p 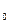 =const, если t -
=const, если t - 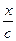 =const, т. е. если х с течением времени изменяется со скоростью с. Таким образом, с — это скорость распространения ударной волны (скорость звука). Решение (7.37) показывает, что распределение давлений, сформированное по х в момент времени t, отвечающее функции f(0-
=const, т. е. если х с течением времени изменяется со скоростью с. Таким образом, с — это скорость распространения ударной волны (скорость звука). Решение (7.37) показывает, что распределение давлений, сформированное по х в момент времени t, отвечающее функции f(0- 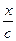 ), остается по форме неизменным во времени, но целиком смещается вдоль оси х со скоростью с. Подставив (7.37) и (7.38) в выражения (7.29) и (7.31), нетрудно показать, что
), остается по форме неизменным во времени, но целиком смещается вдоль оси х со скоростью с. Подставив (7.37) и (7.38) в выражения (7.29) и (7.31), нетрудно показать, что
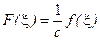
Тогда (7.38) примет вид
 (7.39)
(7.39)
Приравняв (7.37) и (7.39), получим p—p0 = 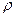 c(
c(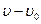 ), а при полной остановке жидкости (
), а при полной остановке жидкости ( 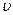 =0) —уравнение (7.28). Во входном сечении, т. е. при х=1, давление во времени не может измениться и р=p
=0) —уравнение (7.28). Во входном сечении, т. е. при х=1, давление во времени не может измениться и р=p 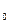 =const. Здесь зарождается отраженная волна
=const. Здесь зарождается отраженная волна 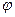 . Из (7.35) следует, что для этого сечения
. Из (7.35) следует, что для этого сечения 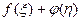 =0 или
=0 или
 (7.40)
(7.40)
т. е. обратная волна 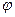 является отражением прямой с переменой знака.
является отражением прямой с переменой знака.
При мгновенном закрытии задвижки (при 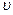 = 0) из (7.39) имеем f =— pc
= 0) из (7.39) имеем f =— pc  , следовательно,
, следовательно, 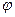 = pc
= pc  . При своем движении вправо волна
. При своем движении вправо волна 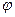 , складываясь с f, дает р — р0 = 0. Волна
, складываясь с f, дает р — р0 = 0. Волна 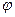 достигнет нулевого сечения за время Т=2l/с, здесь она отражается от заслонки без изменения знака и начинается распространение влево волны разрежения.
достигнет нулевого сечения за время Т=2l/с, здесь она отражается от заслонки без изменения знака и начинается распространение влево волны разрежения.
Если время закрытия задвижки t3<T, то максимальное давление определится уравнением (7.28), а удар называется прямым гидравлическим ударом. Если t3>T, то возникающий при этом гидравлический удар называется непрямым. Максимальный перепад давлений, возникающий при таком ударе, можно найти на основе анализа, аналогичного приведенному выше, и рассчитать по приближенной формуле
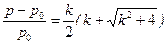
где

|
Выполненный анализ показывает, что давление прямого гидравлического удара не зависит от длины трубопровода и значительно по величине. Так, при течении воды (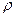 = 10
= 10  кг/м3; с= 1435 м/с) со скоростью
кг/м3; с= 1435 м/с) со скоростью  =1 м/с р — р0 =1,435106 Па
=1 м/с р — р0 =1,435106 Па 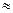 14 ат.
14 ат.
Возможны следующие способы уменьшения ударного давления:
1. Установка запорной арматуры, не допускающей быстрого закрытия трубопровода.
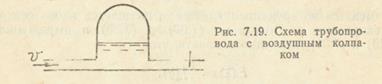
2. Уменьшение инерционных сил путем установки воздушного колпака (рис. 7.19). Здесь время остановки жидкости увеличено за счет сжимаемости газа.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 522; Нарушение авторских прав?; Мы поможем в написании вашей работы!