КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Траекторные углы 2 страница
|
|
|
|
Возможны три различных случая:
- скорость движения источника 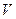 меньше скорости звука в газе
меньше скорости звука в газе  ;
;
- скорость движения источника 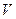 равна скорости звука
равна скорости звука  ;
;
- скорость движения источника 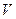 меньше скорости звука
меньше скорости звука  .
.
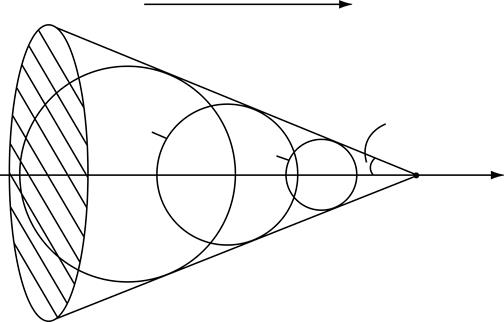
Вне объема ограниченного этой движущейся поверхностью газ покоится (рис. 2.7). Эта поверхность называется головной волной. Головная волна набегает на неподвижный газ и увлекает его за собой, поэтому на поверхности головной волны параметры газа – плотность, давление, скорость, температура – терпят разрыв.
|
|
| |||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
| ||||||||||||||
Рис. 11. Распространение возмущений в сжимаемой среде от точечного источника, движущегося со сверхзвуковой скоростью, относительно среды
Эта коническая поверхность раздела называется поверхностью возмущений (в плоском потоке – линия возмущений, или линия Маха), так как она отделяет возмущенную область газа от невозмущенной.
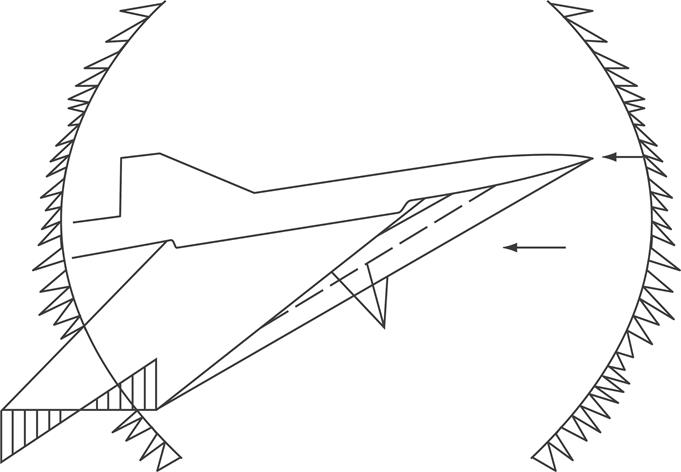
Так как основные параметры газа возмущенной области и в невозмущенной области газа в общем случае качественно различны, то на поверхности линии раздела они терпят разрыв, т.е. меняются скачком.
| |||||||||||||
| |||||||||||||
 | |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
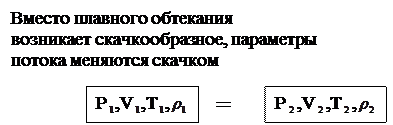 |
Рассмотрим секундный расход жидкости, протекающей через два нормальных сечения  и
и  произвольной трубки тока (рис. 2.1). По определению трубки тока, боковая поверхность жидкости не пропускает.
произвольной трубки тока (рис. 2.1). По определению трубки тока, боковая поверхность жидкости не пропускает.
Следовательно, исходя из закона сохранения массы и непрерывности сплошной среды, можно записать:
 или
или 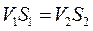 , (8)
, (8)
где  и
и  - соответственно скорости, нормальные сечениям. Из соотношения (2.1) следует важный вывод: скорости потока в несжимаемой жидкости обратно пропорциональны площадям сечений трубки тока. Это означает, что при сужении трубки скорость потока возрастает, при расширении – падает.
- соответственно скорости, нормальные сечениям. Из соотношения (2.1) следует важный вывод: скорости потока в несжимаемой жидкости обратно пропорциональны площадям сечений трубки тока. Это означает, что при сужении трубки скорость потока возрастает, при расширении – падает.
|
|
|
| |||||
| |||||
 |
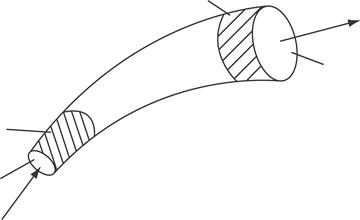
Рис. 12. К выводу уравнения неразрывности и уравнения Бернулли
Кинематическая энергия массы 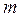 , движущейся со скоростью
, движущейся со скоростью  , в сечении I будет равна
, в сечении I будет равна 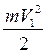 . Аналогично кинематическая энергия той же массы
. Аналогично кинематическая энергия той же массы 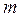 , движущейся со скоростью
, движущейся со скоростью  , в сечении II равна
, в сечении II равна  . Потенциальная энергия давления численно равна работе, совершаемой силами давления на пути, пройденном за единицу времени.
. Потенциальная энергия давления численно равна работе, совершаемой силами давления на пути, пройденном за единицу времени.
Потенциальная энергия давления в сечении I равна  , а в сечении II она равна
, а в сечении II она равна  (где
(где  и
и  - пути, пройденные в единицу времени и численно равные скоростям).
- пути, пройденные в единицу времени и численно равные скоростям).
Так как

то (9)

Это важнейшее уравнение, выражающее закон сохранения механической энергии, называется уравнением Бернулли для несжимаемой невязкой жидкости.
Из уравнения Бернулли следует, что если вдоль трубки тока кинетическая энергия жидкости  увеличивается, то потенциальная энергия
увеличивается, то потенциальная энергия 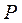 на столько же уменьшается, и наоборот.
на столько же уменьшается, и наоборот.
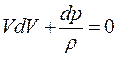 (10)
(10)
Уравнение Бернулли в дифференциальной форме
Уравнения движения газа при сверхзвуковых скоростях
Для определения зависимости изменения скорости потока от площади сечения вдоль трубки тока вернемся к уравнению неразрывности (11):
 (11)
(11)
Используя соотношение, справедливое вдоль трубки тока
 ,
,
и заменяя  (по определению скорости звука), запишем
(по определению скорости звука), запишем
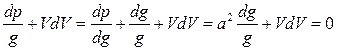 , (12)
, (12)
или
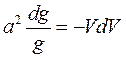 . (13)
. (13)
Разделим и помножим правую часть выражения (13) на 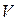 :
:
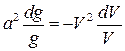 ,
,
или (14)
 .
.
Подставим соотношение (14) в уравнение неразрывности (11):
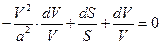 ,
,
или
 .
.
Заменяя 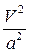 числом
числом 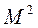 , получаем:
, получаем:
 . (15)
. (15)
Иначе обстоит дело в сверхзвуковом потоке  . В этом случае скобка
. В этом случае скобка 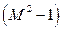 положительна и приращения
положительна и приращения 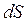 и
и  имеют одинаковые знаки. Таким образом, при увеличении площади сечения поток разгоняется, а при уменьшении – тормозится. И наоборот, разгоняясь, сверхзвуковой поток расширяет трубку тока. В этом принципиальное различие дозвуковых и сверхзвуковых потоков. Наконец, в случае, когда
имеют одинаковые знаки. Таким образом, при увеличении площади сечения поток разгоняется, а при уменьшении – тормозится. И наоборот, разгоняясь, сверхзвуковой поток расширяет трубку тока. В этом принципиальное различие дозвуковых и сверхзвуковых потоков. Наконец, в случае, когда 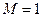 , скобка
, скобка  и, следовательно,
и, следовательно,  =0.
=0.
Таким образом, поток достигает скорости звука в экстремальном значении сечения. Но так как дозвуковой поток разгоняется при уменьшении площади сечения, то скорости звука он может достигнуть в сечении, где площадь минимальна. Из сказанного выше следует важный практический вывод:

|
|
|
| ||||||||
| |||||||||||
| |||||||||||
Рис. 13. Характер течения сжимаемого газа в трубе переменного сечения:
I – дозвуковой поток, скорость постоянная; II – дозвуковой поток сжимается, скорость увеличивается; III – сверхзвуковой поток расширяется, скорость увеличивается; IV – сверхзвуковой поток, скорость постоянна;
V – критическое сечение: скорость потока равна местной скорости звука
Чтобы в трубке переменного сечения достичь сверхзвуковой скорости, необходимо сначала сжать поток, в минимальном сечении получить звуковую скорость, а затем дать потоку расшириться. В расширяющейся части будет получена сверхзвуковая скорость. Труба переменного сечения такого типа называется соплом Лаваля (рис. 13). Сопло Лаваля широко применяется в авиационной технике: в сопловых аппаратах реактивных двигателей, в аэродинамических трубах для получения сверхзвуковых скоростей и т.п.
Взаимодействие между движущимся газом и
телом при наличии вязкости
Теоретически учет влияния внутреннего трения приводит к очень сложным уравнениям, которые могут быть решены только в некоторых частных случаях. Поэтому здесь будут рассмотрены лишь качественные результаты экспериментов и приведены теоретические расчеты, позволяющие понять важную роль влияния вязкости газа на характеристики обтекания тел.
Учет влияния сил трения между слоями газа приводит к появлению качественно нового типа течений – вихревых течений. В вихревом течении газа его частицы могут совершать помимо поступательного, вращательное движение. На вращение частиц тратится дополнительная энергия потока, что приводит, как и следовало ожидать, к появлению дополнительного сопротивления тела.
Помимо появления нового типа течений – вихревых течений, влияние вязкости среды приводит к появлению так называемого пограничного слоя, окружающего обтекаемое тело. Наличие пограничного слоя объясняется появлением сил трения между потоком газа и телом. Вследствие трения на поверхности тела скорость частиц равна нулю относительно тела: газ как бы “прилипает” к телу. В узкой области вблизи тела по направлению, перпендикулярному скорости потока, скорость быстро возрастает до скорости набегающего потока и на расстоянии, называемом толщиной пограничного слоя 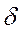 .
.
 | |||||||||||||||
 | |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| |||||||||||||||

Рис. 14. Профиль скоростей в пограничном слое
Скорость на границе пограничного слоя, становится приблизительно равной скорости набегающего потока и не меняется при удалении от тела. Профиль скоростей в пограничном слое приведен на рис. 14.
Таким образом, наличие сил трения приводит к образованию пограничного слоя вокруг обтекаемого тела, пограничный слой “вытесняет” часть внешнего потока и “раздвигает” его вследствие расширения трубок тока. Это обстоятельство приводит к тому, что тело как бы увеличивает свою “толщину” и свой объем в вязком потоке.
Эта условная величина называется толщиной вытеснения пограничного слоя. Физически она характеризует потерю расхода газа, происходящую в пограничном слое из-за наличия сил трения.
Вязкий газ 1 Невязкий газ 2
 | |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
| |||||||||||||||||||
|  | ||||||||||||||||||
| |||||||||||||||||||



Рис. 15. Структура потока в пограничном слое
 - хорда
- хорда
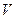 - скорость потока
- скорость потока
 - кинематический коэффициент вязкости
- кинематический коэффициент вязкости
 - расстояние от носка профиля
- расстояние от носка профиля
 - толщина ламинарного слоя в формуле *)
- толщина ламинарного слоя в формуле *)
Ламинарный (что в переводе означает слоистый) пограничный слой – это пограничный слой с плавным изменением профиля скоростей, в котором не происходит перемешивания слоев между собой.
Турбулентным (вихревым) называется пограничный слой, в котором происходит интенсивное перемешивание соседних слоев, профиль скоростей резко меняется во времени и в пространстве, часто имеет нестационарный характер.
Переход ламинарного слоя в турбулентный происходит вследствие потери устойчивости ламинарного течения и зависит от ряда параметров основным из которых является так называемое критическое число Рейнольдса.
В этом слое происходит интенсивное изменение скорости от V =0 на самой поверхности объекта до V=0,99 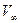 (
( - скорость невозмущенного набегающего потока).
- скорость невозмущенного набегающего потока).
Пограничный слой бывает двух видов ламинарный и турбулентный.
В ламинарном слое (рис. 16) струйки газа текут параллельно друг другу, не пересекаются. Так как они текут параллельно, но с разной скоростью, то силы вязкости (внутреннего трения, молекулярного взаимодействия) действуют только вдоль поверхности струек и относительно малы.
|
|

Рис. 16.
В турбулентном слое струйки пересекаются произвольным образом, происходит интенсивное перемешивание потока, возрастает его интегральная скорость и энергия. Вместе с тем растут силы внутреннего трения.
|
|
 (здесь
(здесь 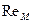 - местное число Rе, см. ниже рис. 17)
- местное число Rе, см. ниже рис. 17)
| |||||||
|
| ||||||
| |||||||

Рис. 17.
Основой для расчёта сопротивления трения является величина коэффициента трения (понятие см. курс физики)  . Общепринятые зависимости для
. Общепринятые зависимости для  , полученные полуэмпирическим путём:
, полученные полуэмпирическим путём:
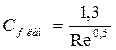
 (17)
(17)
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
 | ||||||||||||||||
| ||||||||||||||||
|
|
|
| |||||||||||||

Рис. 18.
Следовательно, величина сопротивления трения при дозвуковых скоростях, полученная в АДТ более существенно отличается от 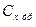 натуры, поскольку различны не только числа Re, но и длины ламинарного и турбулентного участков (см. рис.18 выше). На сверхзвуковых скоростях
натуры, поскольку различны не только числа Re, но и длины ламинарного и турбулентного участков (см. рис.18 выше). На сверхзвуковых скоростях 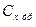 ближе к натуре, поскольку ламинарные участки малы и разница только в числах Re. Поэтому для дозвуковых самолётов поправка, связанная с состоянием пограничного слоя и числом Re, может достигать 10-15%,
ближе к натуре, поскольку ламинарные участки малы и разница только в числах Re. Поэтому для дозвуковых самолётов поправка, связанная с состоянием пограничного слоя и числом Re, может достигать 10-15%,
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 307; Нарушение авторских прав?; Мы поможем в написании вашей работы!





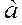
 ,V
,V 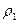
 Ty-144
Ty-144




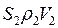


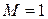






 (16)
(16)


 =10
=10 
 =10
=10