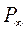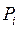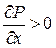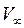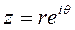КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Траекторные углы 3 страница
|
|
|
|
причём для этого нужно знать длину ламинарного участка на модели
(Для натуры длина ламинарного участка принимается 5%).
Формула для расчёта сопротивления трения:
 (18)
(18)
 - берётся по графику рис. 10 в зависимости от числа Re и соотношения длин ламинарного и турбулентного участков
- берётся по графику рис. 10 в зависимости от числа Re и соотношения длин ламинарного и турбулентного участков
 - коэффициент, учитывающий относительную толщину профиля крыла (рис.19), относительный диаметр фюзеляжа.
- коэффициент, учитывающий относительную толщину профиля крыла (рис.19), относительный диаметр фюзеляжа.
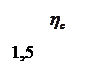 | ||||||||
| ||||||||
| ||||||||
 | ||||||||
| ||||||||

Рис. 19.
Состояние пограничного слоя влияет также на отрыв потока с поверхности тела. Известно, что ламинарный пограничный слой обладает меньшей энергией, чем турбулентный, в частности вследствие меньшей интегральной скорости согласно закону распределения скоростей в пограничном слое (см. рис. 21). Кроме того, эксперименты и теория показывают, что проявление тенденции к отрыву зависит от толщины пограничного слоя любого типа, которая в свою очередь связана с числом Re.
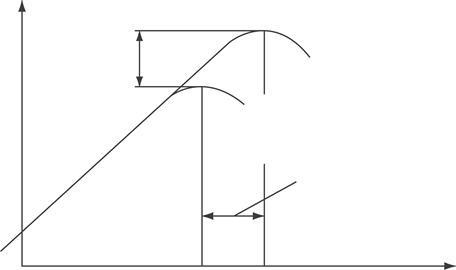
При уменьшении числа Re точка отрыва потока смещается вперед, при этом также уменьшается разрежение в носовой части профиля, что в конечном итоге приводит к потере подъемной и силы (см. рис.20)
|
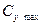 увеличивается на 10-15%,
увеличивается на 10-15%,  увеличивается на 2-3° - рис. 20.
увеличивается на 2-3° - рис. 20.
| |||||||
| |||||||
| |||||||
|
|
|
|
|

| |||||||
| |||||||
| |||||||
| |||||||
Рис. 21. Распределение скоростей
Распределение давления.
Является, пожалуй, вторым по значению типом эксперимента АТД после весовых испытаний. Очевидно, что подъемная сила полностью определяется распределением сил давления по поверхности обтекаемого тела. От этого же частично зависит и сопротивление самолёта  , в которое кроме сил трения
, в которое кроме сил трения
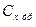 входит слагаемое от сил давления в проекции на скоростную ось Х. Следует также помнить, что силы трения и напряжение трения также зависят от сил нормального давления в каждой точке поверхности крыла, фюзеляжа и пр., поскольку от градиентов давления в первую очередь зависит состояние пограничного слоя.
входит слагаемое от сил давления в проекции на скоростную ось Х. Следует также помнить, что силы трения и напряжение трения также зависят от сил нормального давления в каждой точке поверхности крыла, фюзеляжа и пр., поскольку от градиентов давления в первую очередь зависит состояние пограничного слоя.
|
 Типовая схема модели и методика основных замеров приведена на рис. 22.
Типовая схема модели и методика основных замеров приведена на рис. 22.
| |||||
| |||||
| |||||
Рис. 22. Модель дренированного крыла с дренажными
трубками и манометрами.
2. Развитие отрыва потока.
|
|
| |||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||

Рис. 23.
А - график распределения давления по верхней и нижней поверхности профиля.
Б - профиль крыла с контуром пограничного слоя (увеличено) и профилями скоростей в различных точках верхней поверхности.
I - точка отрыва потока соответствует условию 
II - зона отрыва потока.
 | |||||||||||||||||
| |||||||||||||||||
| |||||||||||||||||
| |||||||||||||||||
| |||||||||||||||||
| |||||||||||||||||
| |||||||||||||||||
 |
| ||||||||||||||||
 | |||||||||||||||||

Рис. 24. Координатная диаграмма 
В передней части профиля имеется отрицательный градиент
давления  . Поток в этой зоне движется в сторону уменьшения давления, очевидно с возрастанием скорости вплоть до точки I. Правее точки I градиент давления становится положительным
. Поток в этой зоне движется в сторону уменьшения давления, очевидно с возрастанием скорости вплоть до точки I. Правее точки I градиент давления становится положительным  , и потоку приходится преодолевать возрастание давления. Возможен либо ламинарный отрыв с последующим прилипанием потока после перехода в турбулентное состояние, просто переход ламинарного пограничного слоя в турбулентный, либо отрыв потока.
, и потоку приходится преодолевать возрастание давления. Возможен либо ламинарный отрыв с последующим прилипанием потока после перехода в турбулентное состояние, просто переход ламинарного пограничного слоя в турбулентный, либо отрыв потока.
Второй участок с большим положительным градиентом давления начинается в 20-30% от конца хорды крыла. Здесь возможен отрыв потока. Условием точки отрыва согласно рис. является 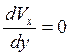 . В зоне отрыва образуется противотечение, она заполнена вихрями.
. В зоне отрыва образуется противотечение, она заполнена вихрями.

Теоретические основы аэродинамики.
Обтекание бывает 2-х видов: потенциальное (безвихревое, безотрывное) и вихревое (срывное). В настоящий момент времени большинство теоретических методов расчёта относится к расчёту потенциального обтекания, и только малая часть методов позволяет, рассчитывать вихревые течения. Существует также принципиальная разница в характере обтекания: при малых скоростях оно •плавное с постепенным искривлением струек до момента непосредственного контакта с телом; при сверхзвуковых скоростях - обтекание ударное со скачкообразным изменением параметров потока - скорости, давления, плотности, температуры. При трансзвуковых скоростях 0,8<М< 1,2 существует смешанный тип обтекания, поэтому в этом диапазоне чисел М расчётные методы дают неточные результаты.
В основе практически всех расчётных методов лежит линейная теория, по которой обтекаемые тела предполагаются слабо искривлёнными, тонкими, а углы атаки - малыми: α=0÷5°.
|
|  |
|
|
|
|

Рис. 25.
Струйки, обтекающие верхнюю и нижнюю образующие тела, имеют разные скорости, как по длине профиля, так и скорость сверху тела отличается от скорости снизу. Для оценки этой несимметрии обтекания вводится понятие циркуляции скорости:
 - элементарная циркуляция (19)
- элементарная циркуляция (19)
 - полная циркуляция по верхней поверхности (20)
- полная циркуляция по верхней поверхности (20)
 - полная циркуляция по нижней поверхности (21)
- полная циркуляция по нижней поверхности (21)
 - суммарная циркуляция скорости по контуру тела.
- суммарная циркуляция скорости по контуру тела.
Из опыта следует, что если тело находится под положительным углом атаки и имеет положительную кривизну, то путь частиц вдоль верхней поверхности профиля больше, если профиль симметричный и угол атаки
α =0, то циркуляции сверху и снизу равны по величине и противоположны по знаку, в этом случае суммарная циркуляция  =0. Для несимметричного течения, как указывалось выше
=0. Для несимметричного течения, как указывалось выше  , т.е.
, т.е.  > 0. Таким образом циркуляция скорости может рассматриваться как мера несимметрии обтекания тела за счёт кривизны и угла атаки.
> 0. Таким образом циркуляция скорости может рассматриваться как мера несимметрии обтекания тела за счёт кривизны и угла атаки.
Теорема Жуковского о подъёмной силе.
Если на тело набегает поток невязкой, несжимаемой жидкости, скорость которого на бесконечности равна 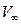 , а циркуляция скорости вокруг тела равна Г, то возникает подъёмная сила
, а циркуляция скорости вокруг тела равна Г, то возникает подъёмная сила
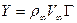 (22)
(22)
|
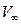 и повёрнутая на 90° относительно
и повёрнутая на 90° относительно 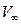 в сторону, обратную циркуляции.
в сторону, обратную циркуляции.
|  |
|  |  |
|

Рис. 26. К пояснению теоремы Жуковского
Поскольку  и
и 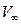 - известные показатели режима полета, основная трудность состоит в определении Г для контура (или тела) произвольной формы. Для простых тел, в частности для круглого цилиндра, выражение для циркуляции известно. Рассмотрим сначала симметричное обтекание цилиндра, которое легко наблюдается в гидротрубе. Очевидно, оно имеет симметричный вид (т.е. Г
- известные показатели режима полета, основная трудность состоит в определении Г для контура (или тела) произвольной формы. Для простых тел, в частности для круглого цилиндра, выражение для циркуляции известно. Рассмотрим сначала симметричное обтекание цилиндра, которое легко наблюдается в гидротрубе. Очевидно, оно имеет симметричный вид (т.е. Г  =0).
=0).
Представим себе теперь обтекание цилиндра, около которого дополнительный циркуляционный поток. Это можно реализовать на специальной установке (рис. 27.) в которой дополнительный расход подкрашенной жидкости подается из внутренней полости цилиндра на его наружную поверхность по касательной к ней через профилированные щели.


Рис. 27. Установка для моделирования несимметричного
обтекания цилиндра.
 При этом симметрия обтекания цилиндра плоско-параллельным потоком нарушается, критические точки А и В, в которых скорость равна нулю, смещаются вверх или вниз относительно оси X (в зависимости от направления циркуляции) - рис. 28.
При этом симметрия обтекания цилиндра плоско-параллельным потоком нарушается, критические точки А и В, в которых скорость равна нулю, смещаются вверх или вниз относительно оси X (в зависимости от направления циркуляции) - рис. 28.
|
|  |
|
|
Рис. 28. Суммирование двух потоков циркуляционного и
плоскопараллельного при несимметричном обтекании цилиндра.
Из теории известна величина Г для цилиндра, критические точки которого находятся под углом  (см. рис. 28. выше).
(см. рис. 28. выше).
 (23)
(23)
Здесь  - радиус цилиндра.
- радиус цилиндра.
 Очевидно, макс. Г будет достигаться при
Очевидно, макс. Г будет достигаться при 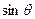 =1, когда совпадут критические точки А и Б. При этом обтекание цилиндра будет иметь вид – рис. 29. B том случае
=1, когда совпадут критические точки А и Б. При этом обтекание цилиндра будет иметь вид – рис. 29. B том случае 

Подставим в выражение для теор. Жуковского значение Г из формулы (23)
 (24)
(24)
Таким образом, что если создать цилиндрическое крыло и обеспечить (непонятно каким путём) угол 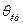 , то задача о подъемной силе решена.
, то задача о подъемной силе решена.
Однако, опыт и природа показывают, что для создания подъемной силы больше применимы достаточно тонкие тела, имеющие небольшое сопротивление, типа профиля крыла птицы.
Определение Г для такого тонкого контура можно произвести, взяв за основу выражение Г для цилиндра и использовав конформное преобразование. Последнее позволяет любую функцию, заданную в плоскости комплексного переменного перевести с помощью некоторой аналитической функции можно перевести в плоскость другого комплексного переменного. Например, окружность с центром в начале координат в компл. пл. записывается уравнением: (величина  при конформном преобразовании сохраняется)
при конформном преобразовании сохраняется)
Уравнение окружности в комплексной форме
|
 (25)
(25)
|
|  |
| ||||||||||
 | |||||||||||||

Рис. 30.
Если взять аналитическую функцию конформного преобразования, предложенную Жуковским
 (26)
(26)
то подставляя (20) в (21) получаем новую комплексную функцию, которая, вследствие условия  не содержит комплексных членов, потому в новой компл. плоскости ε-η представляет отрезок вдоль действительной оси ε. Таким образом, окружность превратилась в отрезок прямой, что уже гораздо ближе к принятым формам несущих поверхностей. Критические точки А и В на рис.54 при симметричном обтекании цилиндра соответствует значениям
не содержит комплексных членов, потому в новой компл. плоскости ε-η представляет отрезок вдоль действительной оси ε. Таким образом, окружность превратилась в отрезок прямой, что уже гораздо ближе к принятым формам несущих поверхностей. Критические точки А и В на рис.54 при симметричном обтекании цилиндра соответствует значениям  =0° и 180°, при этом, соответствующие критические точки в плоскости ε-η получаются на действительной оси при условии
=0° и 180°, при этом, соответствующие критические точки в плоскости ε-η получаются на действительной оси при условии  . Таким образом, длина отрезка действительной оси в плоскости ε-η составляет 4r (рис. 23).
. Таким образом, длина отрезка действительной оси в плоскости ε-η составляет 4r (рис. 23).
 (27)
(27)
|
|  |
|  |  | |||||||||
 | ||||||||||||||


Рис. 31. Исходный цилиндр и прямолинейный отрезок.
Хорошо известно, что путем смещения центра окружности относительно начала координат можно получить путем конформного преобразования различные контуры, в том числе и тонкий, слабо изогнутый профиль с максимальной толщиной, расположенной в передней части и почти круговыми образующими. Именно так строятся так называемые теоретические профили Жуковоского.
|
 Пусть профиль и окружность преобразуются друг в друга как показано
Пусть профиль и окружность преобразуются друг в друга как показано
на рис. 32.
|  |
|  |
|
|
|
|
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 307; Нарушение авторских прав?; Мы поможем в написании вашей работы!




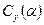 для модели и натуры
для крыльев дозвуковых самолетов.
для модели и натуры
для крыльев дозвуковых самолетов.