Зв'язок ознак, виміряних у номінативних шкалах

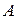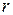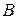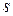Нехай одна з ознак має градацій номінативної шкали, які позначимо відповідно, а ознака має градацій номінативної шкали, які позначимо 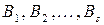. Таблицю

			…		…
			…		…
			…		…
…	…	…	…	…	…	, …
			…		…
…	…	…	…	…	…	…
			…		…

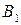
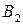
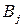
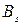
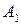
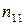
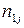
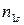
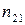
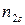
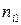
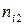
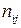
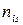
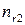
де 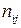— частота появи пари 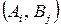в серії спостережень, називають таблицею спряженості.

Якщо досліджувані ознаки незалежні, то незалежними мають бути і події та , тобто

.

Введемо позначення

.

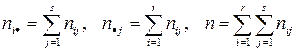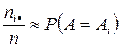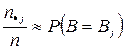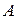Оскільки при достатньо великих п за законом Бернуллі , , а , то незалежність ознак і 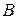, забезпечуватиме виконання рівностей

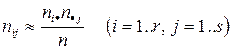
Величини 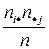називатимемо сподіваними (або теоретичними) частотами розподілу випадкового вектора .

Перевірку узгодженості емпіричного розподілу з теоретичним здійснимо на основі критерію 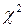. Якщо виконується нульова гіпотеза (ознаки 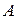і 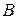— незалежні), то величина

матиме розподіл 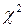з ступенями вільності. Великі значення 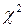у конкретному експерименті свідчитимуть про залежність між ознаками 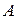і .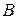

Для оцінки тісноти зв’язку між ознаками Карл Пірсон запропонував величину

,

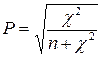яку називають коефіцієнтом спряженості Пірсона. Очевидно, що 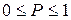, причому для незалежних ознак 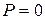. Однак 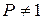, коли таблиця спряженості діагональна (абсолютна залежність ознак 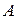і 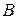). Позбавлений цього недоліку запропонований Кра­ме­ром коефіцієнт

.

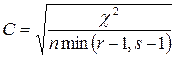Приклад 38 [†]. Розподіл 1725 школярів, класифікованих за їх розумовими здібностями (А — розумово відсталий або повільний і тупий; Б — тупий; В — повільний але розумний; Г — достатньо розумний; Д — явно здібний; Е — дуже здібний) та якістю одягу (одягнений: а — дуже добре; б — добре; в — задовільно; г — погано), наведено в таблиці. Чи існує зв'язок між цими характеристиками?

Здібності Як одягається	А	Б	В	Г	Д	Е
а
б
в
г

Розв’язання: Сформулюємо статистичні гіпотези.

Н ₀: Ознаки незалежні одна з одною.

Н ₁: Ознаки пов’язані між собою.

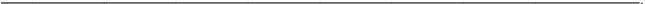
Обчислення статистики 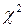проведемо в пакеті Excel. Для цього занесемо дані з умови задачі у блок кліток A1:G5. У блоці B6:G6 обчислимо суми частот по стовпчиках, а у блоці H2:H6 — по рядках. Отримані суми будуть частотами 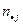, та 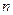відповідно. Щоб обчислити величини , у клітку В7 занесемо формулу =B2^2/B$6/$H2 та скопіюємо її на блок B2:G10. Значення статистики 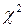знайдемо у клітинці Н11 записавши в ній формулу =(SUM(B7:G10)-1)*H6. У клітинці Н12 знайдемо рівень її значущості, записавши формулу =CHIDIST(H11;15). У клітинці D12 за формулою =SQRT(H11/(H6+H11)) знайдемо коефіцієнт Р, а в клітинці F12 — коефіцієнт С за формулою =SQRT(H11/H6/3). На рис.30 наведено вигляд аркуша MS Excel.

Як бачимо, емпіричне значення статистики 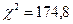і має рівень значущості 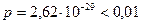. Це дає підстави відхилити нульову гіпотезу і стверджувати, що досліджувані ознаки залежні. Обчислені коефіцієнти Р і С теж будуть статистично відмінними від нуля. Їх величина вказує на не дуже тісний зв'язок між досліджуваними ознаками, однак дати імовірнісну інтерпретацію цих коефіцієнтів важко.

Якщо вхідні дані задані у вигляді таблиці спостережень, то побудувати таблицю спряження та обчислити емпіричні значення статистик і їх рівні значущості у пакеті Statistica 6.0 можна за допомогою субмодуля Tables and banners модуля Basic Statistics/Tables. Вибрати види таблиць спряження (абсолютні чи відносні частоти) та необхідні статистики можна на закладці Option. Для виводу всіх вибраних даних слід натиснути кнопку Detailed two-way tables.

Дата добавления: 2015-05-23