Зв'язок ознак, виміряних у порядкових шкалах

Якщо ознаки Х та Y виміряні у порядкових шкалах, то для дослідника більш суттєвими є не значення , що характеризують і -ий об’єкт 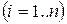, а пари 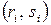, де — ранг серед чисел , а 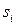— ранг 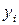серед чисел .

Якщо випадкові величини Х та Y статистично незалежні, то для будь-якої послідовності чисел 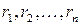всі 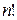перестановок чисел , які відіграватимуть роль рангів є рівноймовірними. У протилежному випадку послідовність 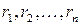буде визначати послідовність тим повніше, чим тісніший зв'язок між величинами Х та Y.

Статистика

відображає близькість рядів 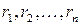і . Вона набуває найменшого значення 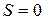лише коли всі (абсолютний прямий зв’язок) і найбільшого — , коли 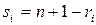(абсолютний зворотній зв'язок). Якщо досліджувані ознаки незалежні, то математичне сподівання статистики 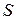дорівнює .

Для зручності імовірнісної інтерпретації замість статистики 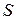розглядають статистику

,

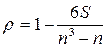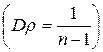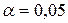яку називають ранговим коефіцієнтом кореляції Спірмена. Ця величина задовольняє нерівність , причому крайні значення досягаються лише у випадку абсолютного прямого чи зворотного зв’язку між рангами. Для незалежних ознак розподілена на відрізку , а її значення концентруються в околі нуля тим щільніше, чим більше п . Критичні значення статистики на рінях значущості та 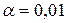для малих п наведені в таблиці 14 додатка. Для великих п величина має розподіл Стьюдента з 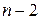ступенями вільності. Емпіричні значення рангового коефіцієнта кореляції Спір­мена, що перевищують за модулем (а тим більше ) є підставою для відхилення гіпотези про незалежність ознак Х та Y і прийняття альтернативної гіпотези.

Якщо при ранжуванні ознак Х та Y зустрічаються однакові ранги, то ранговий коефіцієнт кореляції Спірмена обчислюють за відкоригованою формулою

.

Тут — поправки на однакові ранги для кожної з вибірок, які обчислюють за формулою

,

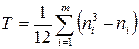де т — кількість груп з однаковими рангами, а — кількість однакових рангів в і -й групі.

В пакеті Statistica 6.0 знаходження рангового коефіцієнта кореляції Спірмена реалізовано у субмодулі Correlations модуля Nonparametrics.

Приклад 39. Трьом групам — вчителі (7 чоловік), учні 8 класу (30 чоловік) та учні 11 класу (17 чоловік) — пропонували оцінити важливість таких рис ідеального вчителя: І – повага до учнів, ІІ –вимогливість, ІІІ – комунікабельність, ІV – прямолінійність, V - терпеливість, VІ – справедливість, VII – самокритичність, VIII - добре знання свого предмета, ІХ – авторитаризм, Х – чесність, ХІ – тактовність, ХІІ - почуття гумору, ХІІІ – консервативність, ХІV - обов'язковість, XV - гуманність. Усереднені по групах дані проранжували. Результати ранжування наведено в таблиці.

Риси	Учителі	Учні 8 класу	Учні 11 класу
І
ІІ
ІІІ
ІV
V
VІ
VII
VIII
ІХ
Х
ХІ
ХІІ
ХІІІ
ХІV
XV

Чи можна стверджувати, що рангові послідовності для кожної з груп взаємопов’язані?

Розв’язання: Сформулюємо статистичні гіпотези.

Н ₀: Рангові послідовності кожної з груп попарно незалежні.

Н ₁: Між парами рангових послідовностей існує кореляційна залежність.

Внесемо дані в пакет Statistica 6.0. У субмодулі Correlations(Spearman, Kendall tau, gamma) модуля Nonparametrics вказуємо, що треба видати детальний звіт (Detailed report у вікні Compute), та вибираємо всі змінні в обох списках. Результати обчислень парних рангових коефіцієнтів Спірмена наведено на рис.31.

Як бачимо, коефіцієнти рангової кореляції між усіма трьома парами ранжувань статистично відмінні від нуля. Це дає підстави відхилити нульову гіпотезу. Оскільки всі три коефіцієнти кореляції достатньо великі, можемо стверджувати, що уявлення про ідеального вчителя в усіх трьох групах узгоджуються.

Приклад 40. За даними прикладу 38 перевірити, чи існує зв'язок між заданими характеристиками, вважаючи, що елементи шкал вимірювання є впорядкованими.

Розв’язання: Сформулюємо статистичні гіпотези.

Н ₀: Ознаки незалежні одна з одною.

Н ₁: Ознаки пов’язані між собою.

Замінивши кожен клас шкали таблиці спряження сукупним рангом об’єктів, що потрапили до цього класу, (з 1 до 130 місця — ранг 65,5, з 131 до 349 — 240 і т.д.), отримаємо таблицю

Здібності Як одягається	65,5
318,5

В пакеті MS Excel обчислимо величини, необхідні для знаходження рангового коефіцієнта кореляції Спірмена та сам коефіцієнт.

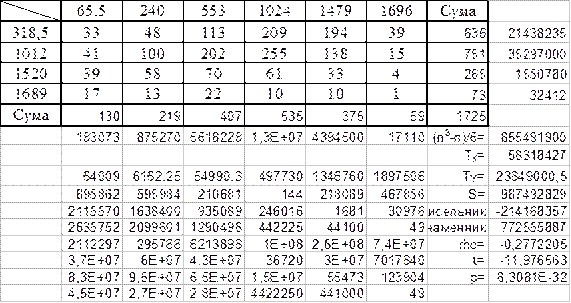
Нижче наведено формули, за якими здійснювались обчислення на цьому аркуші.

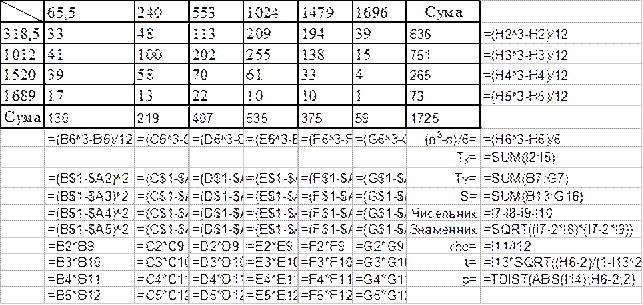
Як бачимо, рівень значущості рангового коефіцієнта кореляції Спірмена 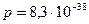істотно менший, ніж 0,01. Це дає підстави відхилити нульову гіпотезу. Оскільки , то можемо стверджувати, що між недбалістю в одязі і розумовими здібностями простежується не дуже тісний зворотний кореляційний зв’язок.

Дата добавления: 2015-05-23