Критерій Фрідмана

Критерій Фрідмана дозволяє перевірити гіпотезу про відсутність відмінності в ріні досліджуваної ознаки для трьох і більше зв’язаних вибірок (тестування однієї групи в різних умовах змушуючого фактора). Альтернативною виступає гіпотеза про наявність такої відмінності.

Статистика Фрідмана обчислюється за формулою

,

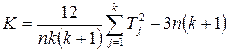де п — кількість об’єктів у групі, k — кількість замірів, що відповідають різним значенням змушуючого фактора, 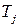— сума рангів для 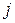-го заміру, отриманих ранжуванням замірів окремо для кожного досліджуваного об’єкта.

Критерій має правосторонню критичну область. Для невеликих вибірок і невеликого k= 3 та k= 4 критичні значення статистики Фрідмана наведено в таблиці 12 додатка. Для великих вибірок статистика має розподіл, близький до 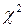з 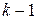ступенем вільності.

Заміри i та j можна вважати попарно різними на спільному рівні значущості a, якщо

,

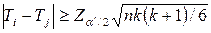де 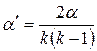і 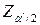— квантиль нормального розподілу рівня .

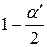У пакеті Statistica 6.0 критерій Фрідмана реалізовано у субмодулі Comparing multiple dep. samples (variables) модуля Nonparametrics.

Приклад 35. З групою з семи учнів протягом двох місяців проводився тренінг, спрямований на зниження їх агресивності. Заміри індексів ворожості (Iv) та агресивності (Ia) за методикою Басса-Даркі у цій групі проведені перед початком тренінгу, після його завершення та через півроку після тренінгу подано в таблиці. Чи можна стверджувати, що тренінг виявився ефективним?

Учень	Iv	Ia
20.02	8.05	30.10	20.02	8.05	30.10
Б-н Наталка
Г-к Тарас
Д-ц Микола
Л-о Марта
С-а Оксана
С-л Юлія
Ш-о Юлія

Розв’язання: Сформулюємо статистичні гіпотези.

Н ₀: Рівні індексу з часом статистично не змінилися.

Н ₁: Відмінності різних замірів рівнів індексів істотні.

Перевірку гіпотез для індексу ворожості проведемо вручну. Подальші дослідження здійснимо з використанням пакету Statistica 6.0.

Для знаходження статистики Фрідмана проранжуємо окремо для кожного учня показники індексу ворожості.

Учень	Iv
20.02	8.05	30.10
Б-н Наталка
Г-к Тарас
Д-ц Микола
Л-о Марта
С-а Оксана		2,5				2,5
С-л Юлія
Ш-о Юлія
Суми рангів		19,5				12,5

Емпіричне значення статистики Фрідмана

.

Критичні значення статистики Фрідмана для 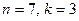дорівнюють 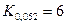, 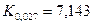. Оскільки , то на цьому рівні значущості нульову гіпотезу можемо відхилити.

Відмінність між замірами можна вважати істотною на рівні значущості 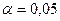, якщо модуль різниці рангових сум перевищує число

.

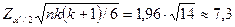У нашому випадку 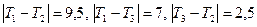, тобто після тренінгу відбувся достовірний зсув рівня індексу ворожості, який з часом не змінився.

Результати перевірки відмінностей індексу агресивності в пакеті Statistica 6.0 наведені на рис. 27. Як бачимо рівень значущості емпіричного значення статистики дорівнює 0,0058 і є істотно меншим, ніж навіть 0,01. Отже, рівні замірів індексу агресивності істотно відрізняються. Далі 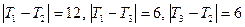. Тобто істотними є відмінності між рівнями індексу агресивності до і відразу після тренінгу. Однак з часом ці відмінності нівелюються. Як бачимо, в цілому тренінг можна вважати ефективним.

Критерій тенденцій Пейджа

Критерій призначений для встановлення тенденції зміни рівня досліджуваної ознаки у зв’язаних вибірках при монотонній зміні вимушуючого фактора.

Нульова гіпотеза стверджує, що рівень досліджуваної ознаки не змінюється при зміні вимушуючого фактора; альтернативною виступає гіпотеза про наявність тенденції зміни досліджуваного рівня при монотонній зміні вимушуючого фактора.

Як і в критерії Фрідмана показники ранжуються для кожного досліджуваного об’єкта. Статистика Пейджа обчислюється за формулою

,

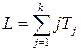де 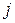— номер вибірки (вибірки нумеруються за монотонною зміною вимушуючого фактора), а 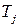— сума рангів її елементів.

Критична область — правостороння. Критичні значення критерію Пейджа для рів­­нів­ значущості 0,05 та 0,01 (кількість елементів у вибірці 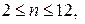кількість значень фактора 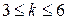) наведено в таблиці 13 додатка. Для визначення критичних точок для великих значень 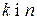використовують статистику

,

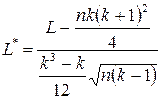яка має близький до стандартного нормального розподіл, якщо справджується нульова гіпотеза.

Приклад 36. Шести студентам-психологам пропонували розв’язати чотири анаграми — терміни. Час їх розв’язання кожним студентом наведено в таблиці. Чи можна стверджувати, що з ростом довжини анаграми зростає час, затрачений на її розв’язання?

Студент	ГАНР	АТСТЬ	ЯЛЕПАД	ПЕРТАРМА
Ірина	2,4	11,0	192,8	262,4
Оксана	3,7	12,9	109,2	214,7
Юрій	2,6	5,3	201,1	197,3
Олена	2,7	6,3	152,4	187,2
Михайло	4,2	3,0	167,4	208,5
Марія	5,2	22,3	187,5	240,4

Розв’язання: Сформулюємо статистичні гіпотези.

Н ₀: Тривалість розв’язання анаграм статистично не відрізняється.

Н ₁: Тривалість розв’язання анаграм достовірно зростає з ростом її довжини.

Для знаходження статистики Пейджа проранжуємо окремо для кожного учня показники часу розв’язання анаграм.

Студент	ГАНР	АТСТЬ	ЯЛЕПАД	ПЕРТАРМА
Ірина	2,4		11,0		192,8		262,4
Оксана	3,7		12,9		109,2		214,7
Юрій	2,6		5,3		201,1		197,3
Олена	2,7		6,3		152,4		187,2
Олег	4,2		3,0		267,4		508,5
Марія	5,2		22,3		187,5		340,4
Суми рангів

Статистика Пейджа дорівнює

.

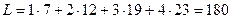Критичні значення статистики для 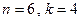дорівнюють 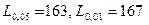. Тому нульова гіпотеза відхиляється. Приймається альтернативна гіпотеза.

Дата добавления: 2015-05-23