Поверхневий натяг. Крайовий кут змочування

Білет 6

Поверхне́вий на́тяг — фізичне явище, суть якого в прагненні рідини скоротити площу своєї поверхні при незмінному об'ємі.

Характеризується коефіцієнтом поверхневого натягу.

Коефіціє́нт поверхне́вого на́тягу — кількісна характеристика поверхневого натягу рідини.

Коефіцієнт поверхневого натягу визначається як сила, що діє з боку рідини на одиницю довжини контуру, що її обмежує. Позначається маленькою літерою гамма γ.

Одиниця вимірювання Н/м або дина/см.

Завдяки силам поверхневого натягу краплі рідини приймають максимально близьку до сферичної форму, виникає капілярний ефект, деякі комахи можуть ходити по воді.

Поверхневий натяг виникає як у випадку поверхні розділу між рідиною й газом, так і у випадку поверхні розділу двох різних рідин.

Своєю появою сили поверхневого натягу завдячують поверхневій енергії.

Поверхне́ва ене́ргія — енергія, яка потрібна на виконання роботи зі збільшення площі поверхні на одиницю.

Вимірюється в Дж/м² або в ерг/см².

Поверхневий натяг призводить до появи додаткового тиску під викривленою поверхнею рідини. Цей тиск визначається рівнянням Юнга-Лапласа

,

де R_x і R_y — два локальні радіуси кривизни поверхні, σ — коефіцієнт поверхневого натягу.

Робота, необхідна для збільшення поверхні рідини:

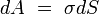
Зміна вільної енергії дорівнює роботі, виконаній над тілом при ізотермічному процесі. Звідти при постійних температурі та тиску, маємо

де 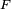є вільною енергію, а є площею поверхні.

Вільна енергія визначається з рівняння , де це — ентальпія та це — ентропія. З цього ми можемо отримати значення частинної похідної ентропії по температурі:

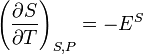
Бачимо, що поверхнева енергія (на відміну від вільної поверхневої енергії) залежить не лише від коефіцієнту поверхневого натягу, а також від його похідної за температурою. Це видно у рівнянні:

Змочування (рос. смачивание, англ. wetting, нім. Benetzung f – дія до властивості змочуваності.

Змочування відбувається, наприклад, при змішуванні корисної копалини, гірської породи тощо з водою, пульпою, реагентом.

Про рідину, яка розпливається тонкою плівкою по твердому тілу, кажуть, що вона змочує дане тверде тіло.

Добре змочування є обов'язковою умовою формування ефективної клейової плівки зв’язуючого на твердій поверхні. Мірою змочуваності твердої поверхні зв’язуючим є крайовий кут змочування θ (див. рис.) - кут, утворений поверхнею розділу двох фаз із поверхнею третьої. Його прийнято відраховувати убік більш полярної (як правило рідкої) фази. Нульове значення крайового кута відповідає повному змочуванню, значення крайового кута θ = 180^о відповідає випадку повного незмочування твердої поверхні зв’язуючим.

2. Закон Ньютона. Рідини, що підпорядковуються закону Ньютона (ньютонівська рідина), та ті, що не підпорядковуються йому (неньютонівські рідини)

Рідина ньютонівська (рос. жидкость ньютоновская; англ. Newtonian (normal) fluid; нім. Newtonsche Flüssigkeit f) – модель рідини, що являє собою суцільне рідке тіло, для якого дотичні напруження внутрішнього тертя τ, спричиненого відносним проковзуванням (зсувом) шарів рідини прямо пропорційні першому степеню градієнта швидкості у напрямі, перпендикулярному до напрямку проковзування:

,

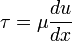де: τ — дотичне напруження внутрішнього тертя, що виникає в рідині, [Па];

μ — коефіцієнт пропорційності або динамічний коефіцієнт в'язкості, [Па·с];

— градієнт швидкості у напрямі, перпендикулярному до напряму зсуву, [с⁻¹].

У загальному випадку у векторному записі: диференціал вектора сили тертя дорівнює добутку коефіцієнта в'язкості та векторного добутку диференціалу вектора площі дотичних шарів рідини і ротора швидкості.^[1]

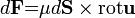
Іншими словами, це означає, що рідина зберігає описану властивість в'язкості незалежно від сил, що діють на неї та швидкостей плину. Наприклад, вода є ньютонівською рідиною, на відміну від неньютонівських рідин, в'язкість яких залежить від швидкості плину а перемішування може призвести до порушення суцільності.

Для ньютонівської рідини в'язкість залежить лише від температури і тиску (а також від хімічного складу) і не залежить від сил, що діють на неї.

Якщо рідину вважати нестискуваною і в'язкість — стала по усьому об'єму рідини, то рівнянням, що описує дотичне напруження в прямокутній системй координат у тензорному записі, буде:

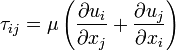
де, згідно з прийнятими позначеннями тензора,

τ _ij — дотичне напруження на i -ій грані елемента рідини в j -ому напрямку;

u_i, u_j — швидкість в i -ому та j -ому напрямках;

x_i, x_j — i -а та j -а координати напрямків.

Якщо рідини не описуються наведеними рівняннями, то їх називають неньютонівськими рідинами, до яких відносяться, наприклад, розчини та розплави полімерів, низка твердих суспензій та більшість рідин великої в'язкості.

При русі шарів рідини з різними швидкостями між ними виникають сили внутрішнього тертя F_тер, або сили в’язкості. Течія ідеально в’язких тіл (рідин) описується законом Ньютона:

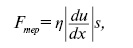(1)

де 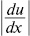— модуль градієнта швидкості в напрямі х, перпендикулярному напряму руху u шарів; s — площа зіткнення шарів; η — коефіцієнт внутрішнього тертя, або динамічна в’язкість.

Дата добавления: 2015-05-24