
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системи числення (1)
|
|
|
|
Вправи
Запитання
1. Що таке вислів і алгебра висловів?
2. Які є логічні сталі?
3. Які ви знаєте основні логічні операції?
4. Який пріоритет логічних операцій?
5. Для чого використовуються логічні формули?
6. Що таке автомат?
7. Які є етапи створення автомата?
1. Які вислови є істинними, а які — хибними:
а) «сьогодні 10 жовтня»; б) «доба має 24 години»;
в) «завтра буде урок інформатики»; г) «Х > 10», якщо Х = 20;
д) «X < 100», якщо Х = 200; д) «надворі дощ»?
Записати відповіді у вигляді ланцюжка з 6 бітів.
2. Доведіть властивості, побудувавши відповідні таблиці істинності:
а) А + 1 = 1; б) А • 0 = 0; в) A + 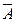 = 1; г) А •
= 1; г) А • 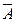 = 0;
= 0;
д) А + B = B + А.
3. Перевірте правильність другої формули де Моргана.
4. Дано логічні формули автоматів:
4.1)D=А·B; 4.2)D=А+С; 4.3) В =А +B + 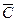 .
.
Якого значення набуде змінна D, якщо:
а) А = 0, B = 0, С = 1; б) А = 0, B = 1, С = 1;
в)А= 1, B = 1, С = 1; г)А= 0, B =0, С= 0;
д)А = 1, B = 0, С = О?
Запишіть відповіді у вигляді ланцюжка з 5 бітів.
5. Спростіть логічні вирази:
а) А +А • B; б) 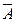 • B + 1; в) A • B + А • С +А;г) А •
• B + 1; в) A • B + А • С +А;г) А • 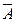 + B •
+ B • 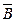 ;
;
д) А • 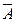 + А •
+ А • 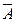 .
.
6. Спростіть логічні вирази:
а) А • B • А + B • А • B; б) А • B • (А + 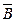 ); в) А + B •
); в) А + B • 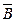 +
+ 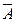 ;
;
г) (А + 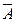 ) (А • B + А); д) А • B • С+А • B •
) (А • B + А); д) А • B • С+А • B • 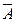 +B • С • B.
+B • С • B.
7. Побудуйте таблицю істинності логічної операції D = А • B • С.
8. Дано логічну формулу автомата: D=А · B · 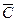 +
+ 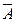 · B · С+
· B · С+ 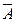 ·
· 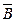 .
.
Чи буде сигнал на виходіD, якщо:
а) А = 0, B = 0, С = 1; б) А = 0, B = 1, С = 1;
в) А = 1, B = 1, С = 1; г)А = 0, B = 0, С= 0;
д) А = 1, B = 0, С= О?
Запишіть відповіді у вигляді ланцюжка з 5 бітів. ___
9. Нарисуйте хеми автоматів, заданих формулами:
а)С= 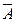 •
• 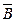 +А • B;
+А • B;
б)С= 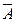 • B+А •
• B+А • 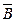 ; в)D = А · B •
; в)D = А · B • 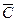 +
+ 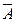 •
• 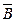 • С+А ·
• С+А · 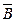 .
.
10. Змагання судять троє суддів. Якщо суддя вважає, що слід призначити штрафний удар, він натискає на кнопку (подає сигнал на вхід автомата). Головний суддя має кнопку А, два інші — кнопки B і С. На табло з'явиться повідомлення «ШТРАФНИЙ УДАР» і пролунає свисток (це сигнал на виході автомата), якщо рішення прийнято трьома суддями, або двома, серед яких є головний суддя. Складіть логічну формулу і функціональну (фізичну) схему автомата.
11. Розв'яжіть логічну задачу про тендер комп'ютерних фірм, якщо другий прогноз був таким: ІВМ —друге місце, АРРLЕ —третє.
1. Поняття про системи числення. Десять пальців рук — це перший пристрій для рахунків, яким людина користується з доісторичних часів. Число 10 стало основою десяткової системи числення, алфавіт якої складається з десяти цифр: від 0 до 9.
У різні історичні періоди користувалися також системами числення, відмінними від десяткової. Широко застосовували дванадцяткову систему. Її походження пов'язують з рахунками на чотирьох вказівних пальцях руки, які мають 12 фаланг. До нашого часу ця система дійшла у словах «дюжина», «грос»— дюжина дюжин, «маса» — дюжина гросів, 1 фут =12 дюймів, 1 шилінг =12 пенсів. У давньому Вавилоні діяла шістдесяткова система числення. Її ми використовуємо і сьогодні. Наприклад, 1 година = 60 хвилин, 1 хвилина = 60 секунд, 1 градус = 60 хвилин. Є змішані системи числення. Наприклад, 1 доба = 24 години, 1 година = 60 хвилин і т. ін. Деякі африканські народи користувались п'ятірковою системою числення, а ацтеки і майя — двадцятковою.
Задача 1. Скільком одиницям дорівнюють 2 гроси?
Розв'язування. 2 гроси = 2 · 12 · 12 = 288.
Система числення — це алфавіт системи та правила утворення чисел і дій з ними. Системи числення є позиційними або непозиційними.
2. Позиційні системи числення. У позиційній системі значення цифри залежить від позиції, яку цифра займає в зображенні числа. У цілих числах позиції нумерують справа наліво, починаючи з нульової.
Наприклад, у числі 4321 остання цифра 1 перебуває у нульовій позиції й означає кількість одиниць; передостання цифра 2 стоїть у першій позиції й означає кількість десятків (у нашому випадку — це 2 десятки) і т. ін. Отже, число 4321 можна записати у вигляді такої суми:
4321 = 4 · 1000 + 3 · 100 + 2 · 10 + 1 = 4 · 103 + 3 · 102 + 2 · 101 + 1 · 100.
Щоб означити, що число належить саме до десяткової системи числення, пишуть (4321)10. Число 10 є основою десяткової системи числення.
Розглянемо системи числення з основами, відмінними від 10.
Алфавіт системи числення з основою р. Алфавіт системи числення з основою р складається з р цифр: 0, 1, 2,..., р-1.
Інші цифри використовувати не можна. Найчастіше застосовують системи числення з основами 2, 8, 10, 16.
Відомо, що у десятковій системі алфавіт складається з таких цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9. У системі числення з основою р = 8 алфавіт такий: 0, 1, 2, 3, 4, 5, 6, 7.
У двійковій системі числення р = 2. Алфавіт системи складається з двох цифр: 0, 1. Приклади двійкових чисел: (110011)2, (1110001)2, (101)2,.
Десяткове значення двійкового числа вигляду (аk аk -1...а1 a0)2, визначають за формулою
(аk аk -1...а1 a0)2 =а k • 2k+аk -1 • 2k –1 +...+ а1 · 2 + а0.
Наведемо приклади двійкових чисел та їхні десяткові значення:
(1)2 =1-2°=1;
(10)2 = 1 • 21 + 0 • 2° = 2;
(11)2 =1 · 21 + 1 · 20=3;
(100)2 = 1 • 22 + 0 • 21 + 0 • 2° = 4;
(101)2 = 1 • 22 + 0 • 21 + 1 • 2° = 5;
(110)2 = 1 • 22 + 1 • 21 +0 • 2° = 6;
(111)2 =1 · 22 + 1 · 21 + 1 · 20 = 7;
(1000)2 = 1 • 23 + 0 • 22 + 0 • 21 + 0 • 2° = 8.
3. Переведення чисел з системи числення з основою р у десяткову систему. Розглянемо формулу, яка описує правило переведення цілих чисел із системи числення з основою р, зокрема двійкових (якщо р= 2), у числа десяткової системи: (аk аk -1...а1 a0)p = аk pk +аk –1 · pk – 1 +... + а1· p+ a0.
Як приклад розглянемо переведення чисел з вісімкової системи у десяткову:
(аk аk -1...а1 a0)8 =аk • 8 k + аk –1 • 8 k – 1 +...+ а1 · 8 + а0;
(37)8 = 3 · 81 + 7 = 24 + 7 = 31;
(4321)8 =4 • 83 + 3 • 82 + 2 · 8 + 1 = 2048+192+16+1=2257;
З а дача 2. Двійковий код символа пересилається від клавіатури в пам'ять восьмирозрядною шиною. Провідники в шині пронумеровані від 0 до 7. Визначити десяткове значення коду, якщо відомо, що напруга є в першому, третьому і шостому провідниках.
| Номер провідника | Наявність сигналу | Код |
| Немає | ||
| Є | ||
| Немає | ||
| Немає | ||
| Є | ||
| Немає | ||
| Є | ||
| Немає |
Отже, десяткове значення коду таке:(01001010)2 = 26 + 23 + 21 = 64+8+2 = 74.
З таблиці кодів АSСІІ можна визначити, що цим символом є літера < І.
4. Переведення чисел з десяткової системи в іншу. Будь-якедесяткове число можна записати в іншій системі числення, наприклад, у вісімковій, двійковій тощо.
Правило. Щоб перевести ціле число з десяткової системи в систему з основою р, треба виконати послідовне ділення цього числа на число р за таким алгоритмом.
1. Число поділити без остачі на р.
2. Визначити остачу і частку.
3. Якщо частка менша за р, то виконати пункт 6, якщо ні, то виконати пункт 4.
4. Розглянути частку як нове число.
5. Виконати пункти 1,2,3.
6. Прочитати результат.
Результат — це послідовність цифр, що складається з останньої частки та всіх остач, починаючи від останньої.
Приклад 1. Перевести (125)10 у вісімкову систему числення.
 |  |
Результат: (175)8.
Ділення рекомендують виконувати так:
 |
Переведення цілих чисел у двійкову систему виконуютьу дваетапи:
1) спочатку переводять десяткове число в систему з основою p =8;
2) отримане число переводять у двійкову систему.
Щоб перевести число з вісімкової системи у двійкову, використовують наступну таблицю кодів (рис. 1.9).
Рис. 1.9. Таблиця двійкових кодів чисел від0 до 7
Користуючись таблицею, замінюють цифри у вісімковому числі відповідними двійковими кодами. Отримують шукане двійкове число.
Наприклад, (175)8 = (001 111 101)2 = (1111101)2.
Нулі на початку числа можна відкинути. Нулі у кінці числа відкидати не можна.
Отже, (125)10 =(1111101)2.
Перевіримо, чи дорівнює отримане двійковечисло (125)10:
(1111101)2 = 1 · 26 + 1 · 25 + 1· 24 + 1 · 23 + 1 · 22 + 1 · 21 + 1 · 20=
=64+32 +16+8+4+0+1= 125.
Довідка 1. Для переведення десяткових чисел у двійкову систему можна
користуватися і наведеним вище правилом для значення р=2, але такий спосіб є громіздким.
З а д а ч а З*. Розглянемо панель керування літальним апаратом з тумблерами-перемикачами. Перемикачі мають номери від 0 до 7 (зліва на право). За допомогою такої панелі можна подати 256 різних команд. Ось десяткові коди деяких з них: 125—зліт; 126—посадка; 127—гальмування; 128— негайна зупинка; 129— рівномірне прискорення; 130— увімкнути прожектор; 131— вимкнути прожектор. Які перемикачі потрібно увімкнути, щоб подати команду а) «посадка»; б) «негайна зупинка»?
Розв'язування. У випадку завдання а) відповідь дасть двійкове зображення числа 126. А саме, якщо у деякій позиції відповідного двійкового числа буде одиниця, то треба увімкнути перемикач, що має номер цієї позиції, якщо ж буде нуль, то перемикач вмикати не треба.
Двійкове число можна визначити за правилом ділення або методом підбору так: число 126 складемо з чисел 64, 32, 16, 8, 4, 2, 1:
126= 64 +32 + 16 + 8+ 4 + 2 = 26 + 25 + 24 + 23 + 22 + 21 = (01111110)2 .
Отже, потрібно увімкнути перемикачі з номерами 1,2,3,4,5,6.
У випадку завдання б) потрібно увімнути 7-й перемикач, бо 128 = 27 = (10000000)2 - одиниця стоїть у сьомій позиції двійкового коду.
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 698; Нарушение авторских прав?; Мы поможем в написании вашей работы!