Лінійна інтерполяція

Вбудовані функції MathCAD дозволяють при інтерполяції проводити через експериментальні точки криві різної степені гладкості.

При лінійній інтерполяції апроксимуюча функція поєднує

досліджувальні точки відрізками прямих ліній. Для лінійної ін- терполяції використовується вбудована функція linterp.

Синтаксис функції:

l int erp (x, y, t), де x – вектор досліджу

вальних значень аргумента; y – вектор досліджувальних зна- чень функції; t – значення аргумента, при якому обчислюються інтерполюючі значення функції. Іноді необхідно задати одне ін-

терполююче значення функції, але частіше визначається ряд

значень функції, тоді t – вектор значень, а результат розрахун- ків – масив інтерполюючих значень. Частіше t – просто змінна

(аргумент інтерполюючої функції), тоді результат розрахунків – функція, яку можливо подальше інтегрувати, диференціювати та інше.

Приклад У таблиці наведені дані залежності те- мператури кипіння нітробензолу від тиску. Необхідно знайти температури кипіння нітробензолу від тиску при значенні тиску Р = 30; 50; 70; 300; 500 мм. рт. ст., відсутніх у таблиці.

Таблиця– Залежність температури кипіння нітробе- нзолу від тиску

Р, мм. рт. ст.
t, °C	84.6	99.3	115.4	125.8	139.9	161.2	185.8	210.6

Для розв’язку даної задачі необхідно побудувати графік

залежності тиску від температури та з нього знайти значення

температури кипіння при потрібних значеннях тиску. Тут необ- хідно для побудови графіка скористатися лінійною інтерполяці- єю.

Розв’язок задачі та приклад лінійної інтерполяції зображе-

ні на рис.

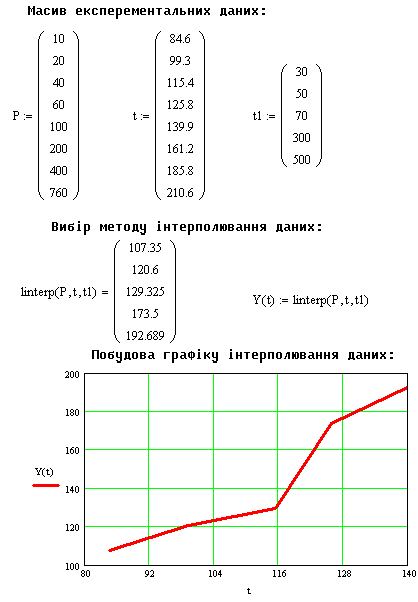
Рисунок

Дата добавления: 2015-05-24