Метричний тензор у косокутних координатах 2 страница

Нам залишається ще знайти вираз для оператора Лапласа в косокутних координатах. Будемо виходити з формули

Δ= 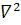. тоді

= = ,

І остаточно Δ = .

У випадку декартової системи = і /20.7/ зводиться до відомого виразу Δ = = .

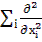Метод важливіший від відкриття,тому що правильний метод дослідження приведе нас до нових, ще більш цінних відкриттів.

Л. Ландау

21. Перетворення координат і компонент вектора при переході від однієї косокутної системи до іншої

Здійснимо перехід від косокутної системи до 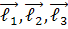до нової системи

. Простір будемо вважати лінійним, отже вектори повинні бути пов’язані лінійними співвідношеннями

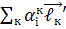= , і= 1,2,3 /21.1/

= , к = 1,2,3 /21.2/

З'ясуємо геометричний зміст коефіцієнтів

і . Приймемо в /21.1/ і =1, тоді

= + + .

Рис. 63 Довільний вектор 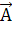можна розкласти по трьох напрямках = + + ,

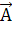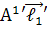-72-

Отже /21.1'/ - це формула розкладу вектора по напрямках нових масштабних векторів. Звідси зрозуміло, що - це узагальнена складова вектора по напрямку вектора , - узагальнена складова вектора по напрямку 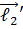. Взагалі, 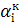- це узагальнена складова вектора по напрямку .

Аналогічно, - це узагальнена складова вектора по напрямку .

Розглянемо довільний вектор 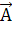і обидві сторони /21.1/ і /21.2/ помножимо скалярно на 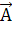. Маємо

= , і= 1,2,3

= , к = 1,2,3

Тут = 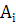- узагальнені проекції вектора у старій системі,

= – узагальнені проекції вектора 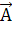в новій системі. Таким чином,

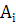= , і= 1,2,3 /21.3/

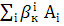= , к = 1,2,3 /21.4/

Формули /21.3/ і /21.4/ дають закон, за яким перетворюються узагаль-нені проекції від однієї косокутної системи до іншої. Іншими словами,

/21.3/ і /21.4/ визначають трансформа-ційні властивості узагальнених проекцій вектора.

Узагальнені проекції вектора будемо називати називати його коваріантними складовими.

На рис. 64 показано як змінюються Рис. 64 коваріантні складові вектора при при переході від однієї системи до іншої. для простоти розглянемо дві плоскі системи, визначені одиничними масштабними векторами.

Знайдемо закон перетворення узагальнених складових вектора. У формулу 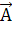= підставимо /21.1/. Одержимо

-73-

= .

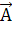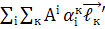З другого боку, вектор 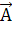можна розкласти по масштабних векторах нової системи = .

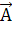Порівнюючи вирази для 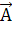знайдемо

' = . к = 1,2,3 /21.5/

Аналогічно = '. і = 1,2,3 /21.6/

Узагальнені складові вектора називають його контраваріантними складовими. Формули /21.5/ і /21.6/ визначають трансформаційні властивості контраваріантних складових вектора.

Легко завважити,що контраваріантні складові вектора перетворюються за іншим законом,ніж його коваріантні складові. Дійсно,розписуючи /21.3/, одержимо.

= + +

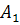= + + /21.3'/

= + +

А формули /21.6/ мають вигляд

= + +

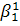
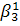
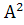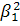
= + + /21.6'/

= + +

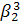
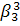
У випадку декартових координат очевидно = ,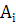

=

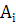І тому = = = ).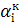

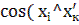Формули /21.1/ і /21.2/ визначають трансформаційні властивості масштаб-них векторів. Знайдемо подібні формули для дуальних векторів. Для цього досить записати /21.5/ і /21.6/ у вигляді

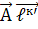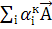
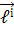= , і =1,2,3

= , к =1,2,3 а звідси випливає, що

-74-

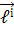= к =1,2,3 /21.7/

= і =1,2,3 /21.8/

У формулі /21.8/ пере позначимо рухомий і німий індекс

=

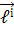І розглянемо добуток 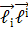. використовуючи /21.1/ одержимо

= .

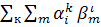
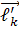
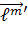Тут = , = ,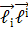

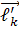
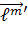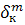Отже, = = .

Таким чином, коефіцієнти 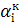і не є незалежними - вони пов’язані дев'ятьма співвідношеннями

= . і,ι = 1,2,3 /21.9/

Цю рівність можна записати і в іншому вигляді. виходячи з формул /21.7/ і /21.2/, маємо

= , =

= = ,

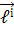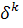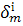А пере позначуючи індекс одержимо

= і,ι = 1,2,3 /21.10/

У випадку декартових координат 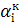= = і ми приходимо до формул /1.12/ і /1.10/.

На випадковість при великих відкриттях

натрапляють лише ті, хто її вартий.

Ж. Лагранж

22. Скаляри, вектори і тензори в косокутній системі координат

У математиці і фізиці розрізняють дві групи величин: інваріантні і варіантні.

-75-

Інваріантом /скаляром/ називають величину, яка не змінюється при переході від однієї системи координат до іншої. Приклади: дивергенції вектора, скалярний добуток двох векторів, температура тіла та ін.

Варіантні величини – це величини, що змінюються за певним законом при переході від однієї системи координат до іншої. Варіантними величинами є компоненти вектора, а також більш складні величини – компоненти тензора.

Означення:Три величини називаються коваріантними складовими вектора, якщо при переході від однієї косокутної системи до іншої вони перетворюються за законом

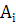= , і = 1,2,3 /22.1/

= , к= 1,2,3 /22.2/

Означення2:Три величини називаються коваріантними скла-довими вектора, якщо при переході від однієї косокутної системи до іншої вони перетворюються за законом

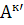= , к = 1,2,3 /22.3/

= , і= 1,2,3 /22.4/

Таким чином, вектор має три коваріантні і три контрваріантні складові. Вони пов’язані між собою за допомогою матричного тензора.

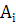= = і = 1,2,3 /22.5/

Очевидно, в декартовій системі координат

= = = .

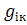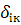
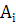Виявляється, що існують величини більш складні ніж вектори і їх компоненти. Розглянемо два вектори 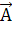і та їх коваріантні складові 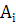(і =1,2,3), = (j = 1,2,3). Утворимо так званий мішаний добуток

. і,j =1,2,3

Це сукупність дев'яти величин, що перетворюються за певним законом при переході від однієї системи до іншої. Цей закон має вигляд

= тобто =

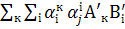
-76-

Припустимо, що існують величини, які мають дев’ять компонент, але не обов’язково є мішаними добутками. Закон їх перетворення такий:

(22.7)

такі девять величин називають коваріантними складовими тензора другого рангу.

Формули зворотнього перетворення для коварінтних складових тензора другого рангу знайдемо виходячи з формул

Тоді

к,і=1,2,3 (22.8)
Поняття тензора є більш складним ніж поняття вектора. Вектор можна інтерпретувати геометрично як відрізок, що має довжину і напрям, або зобразити його як рядок з його компонент Тензор другого рангу можна представити з допомогою матриці

(22.9)

Розглянемо мішані добутки контраваріатних складових двох векторів А^і і В^j , для яких закон перетворення має вигляд

і,j=1,2,3 (22.10)

к,і=1,2,3 (22.11)

Аналогічно можна про дев’ять величин Т^{і j}, які мають такий же закон перетворення

Будемо їх називати котраваріантними складовими тензора другого рангу. Вони визначають матрицю

-77-

Нарешті, за аналогію з мішаним добутком А_і В^j , можна говорити про мішані компоненти тензора другого рангу 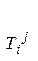, їх трансформаційні властивості мають вигляд

і,j=1,2,3 (22.12)

к,і=1,2,3 (22.13)
Таким чином, тензор другого рангу маэ девять коварыантних складових Тij, дев’ять контраваріатних складових Ті j і дев’ять мішаних складових 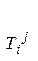. Зв’язок між ними здійснюється за допомогою операцій опускання і піднімання індексів

Застосовуючи цю операцію два рази, ми можемо написати

Зауважимо, що при опусканні чи підніманні індексів тензора потрібна обережність. Опускаючи в тензора 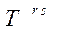індекс S одержимо мішаний тензор опускаючи індекс r одержимо мішаний тензор . При цьому, взагалі кажучи,

Власне тому доцільно, місце, з якого опущено індекс, позначати точкою. Виняток становлять симетричні тензори, коли порядок індексів не має значення. Очевидно, що аналогічно спостерігається і при підніманні індексів коваріантних складових тензора

Тепер можна ввести поняття про тензори третього і вищих рангів. Трансформаційні властивості складових тензора третього рангу визначаються за формулами

-78-

Зв'язок між ко- і котривіальними складовими здійснюється за допомогою операцій опускання і піднімання індексів.

Даємо тепер загальне ьозначення:

Тензором рангу N, що має N₁ коваріантних і N₂ коваріантних складових / N₁+ N₂= N/, називають сукупністю 3^N величин, які при переході від однієї косокутної системи до іншої перетворюються за законом

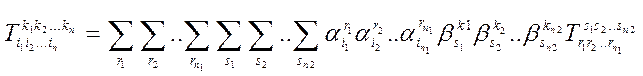
Кількість коваріантних чи контрваріантних індексів можна змінювати за допомогою операцій спускання чи піднімання індексів.

Наприклад,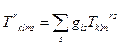

Згідно з загальним означенням, вектор можна трактувати, як тенвектор рангу N₁, скаляр – як тензор рангу N = 0.

Перерахуємо деякі загальні властивості тензорів:

1/ добуток тензора на стале число є тензором цього ж рангу;

2/ сума двох тензорів є також тензором цього ж рангу

Очевидно, що обидва доданки повиння мати однакову кількість верхніх індексів і відповідно однакову кількість нижніх індексів, тобто обидва доданки повинні мати однакову тензорну розмірність;

3/ добуток двох тензорних рангів N і M є тензером рангу N + M.

Перевіримо правильність цієї теореми для добутку двох тензорів і , тобто переконаємось, добуток є мішаним тензором шостого рангу. Для цього досить записати трансформаційні властивості тензорів Т і

і тоді

Права сторона цієї рівності і дає закон перетворення мішаного тензора шостого рангу.

Дамо два важливі означення.

1. Тензор 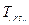називається симетричним відносно індексів 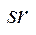якщо значення його компонент не змінюється при перестановці індексів

-79-

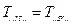
Зокрема для симетричного тензора другого рангу виконується умова

2. Тензор 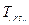називають антисиметричним відносно індексів 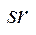якщо

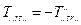
Компоненти асиметричного тензора другого рангу задовольняються умові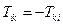

Якщо симетричними є коваріантні складові тензора, то і відповідні контраваріантні складові є симетричними. Наприклад, для тензора другого рангу ми маємо

Аналогічно, якщо -ф-

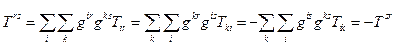
Теорема. Довільний тензор другого рангу завжди можна записати як суму двох тензорів: симетричного і антисиметричного.

Доведення цієї теореми випливає з очевидної рівності

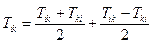
Тут додаток є симетричним, а антисиметричним виразом.

Цю теорему легко узагальнити на довільну пару індексів тензора будь якого рангу.

Спростимо нашу термінологію. Коли задані коваріантні складові вектора ми будемо говорити, що заданий коваріантний вектор Аналогічно, коли йдеться про контрваріантний вектор ми маємо на увазі контрваріантні складові цього вектора. Взагалі, мова йтиме про коваріантний тензор ,контрваріантний тензор 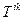, мішаний тензор 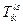. При цьому матимемо на увазі відповідно коваріантні, контрваріантні і мішані складові тензора Т.

Дата добавления: 2015-05-24