Метричний тензор у косокутних координатах 5 страница

Метричний простір, для якого

називають ортогональним. Як легко перевірити, для такого простору

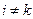
Розглянемо довільний вектор 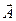у точці метричного простору, визначеній координатами 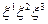. Його ко- і контраваріантні складові це відповідно узагальнені проекції і узагальнені складові по напрямках векторів локального репера. Їх трансформаційні властивості визначаються формулами (30.3) – (30.4) і (30.7) – (30,8). Зв'язок між ними здійснюється за допомогою операцій піднімання і опускання індекса

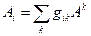, (31.6)

Шість, маленьке два,

хрестик і закарлючка.

Господи, от голова була…

Скільки тут таємниць…

Уееллс. Людина-невидимка

32. Задача про паралельне перенесення вектора

Ми з’ясували, що звичайні похідні від скалярного поля є складовими коваріантного

-108-

векторного поля. Однак, вже мішані похідні від векторного поля, і тим більше мішані похідні від тензорного поля другого і вищих рангів, не утворюють тензорного поля в криволінійному просторі.

Наша задача полягає в тому, щоб одержати нові тензорні поля в результаті диференціювання, тобто нам треба розробити такий метод диференціювання тензора, який приводить до тензорів вищих рангів.

Попередньо нам треба розв’язати доволі складну задачу про паралельне перенесення вектора. Загальності будемо розглядати вектор 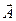у метричному просторі, визначеному метричним тензором .

Кожній точці простору відповідає свій локальний репер, визначений векторами . Дійсно, якщо заданий тензор ми завжди знайдемо довжину векторів

і кути між ними

.

Перенесемо паралельно вектор 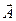з точки в нескінченно близьку точку . Очевидно, сам вектор не зміниться, однак його ко- і контраваріантні складові змінюються за рахунок зміни репера. Ці зміни позначимо відповідно через і .

Зробимо цілком логічне припущення: зміна складової вектора повинна бути однорідною квадратичною функцією складових вектора і диференціалів координат

(32.1)

(32.2)

де і – набори якихось невідомих коефіцієнтів.

Переконаємось насамперед, що

Для цього розглянемо згортку двох векторів 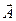і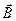

і перенесемо паралельно обидва вектори з точки у точку

-109-

Підставимо сюди вирази (32.1) і (32.2)

.

В другому члені правої сторони цієї рівності пере позначимо німі індекси 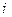і (індекс замінимо на , індекс – на 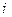), тоді

.

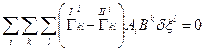Тому що – довільні, ми і одержуємо (32.3)

Таким чином, закон паралельного перенесення вектора можна записати у вигляді

(32.4)

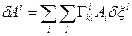(32.5)

Поки що ми знаємо про коефіцієнти , тільки те, що вони є функціями координат

(32.6)

Знайдемо їх трансформаційні властивості.

Перейдемо від системи до нової системи . У новій системі

Перепозначимо індекси сумування в останній групі доданків, тоді

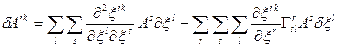(32.8)

-110-

Підставляючи у формулу (32.7)

, ,

одержимо

(32.9)

Праві сторони (32.8) і (32.9) мусять збігатися, бо

Величини і довільні, тому вираз у фігурній дужці дорівнює нулеві. Отже,

.

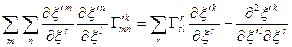Щоб знайти вираз помножимо одержану рівність на і просумуємо результат по і , тоді

Таким чином,

Перетворимо ще останню групу доданків

Остаточно закон перетворення коефіцієнтів має вигляд

(32.10)

Формула (32.10) у правй частині має дві групи доданків. Перша група має такий же вигляд, як закон перетворення мішаного тензора

-111-

третього рангу. Вираз

не залежить від 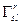і симетричний відносно долішніх індексів. Наявність цього виразу свідчить про те, що 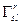не є тензором.

Якщо існує така система координат, в якій

то

Тоді рівність

залишається справедливою в усіх інших координатних системах. Для цього досить, щоб у метричному просторі можна було ввести таку систему координат, в якій хоча б локально.

Величини називають коефіцієнтом афінного зв’язку. Якщо

(32.11)

афінний зв'язок називають симетричним. Далі ми обмежимось розглядом тільки симетричного афінного зв’язку.

Наш досвід переконує нас, що природа – це реалізація найпростіших математичних ідей.

А. Ейнштейн

33. Символи Крістоффеля. Класифікація просторів

Величини можна визначити однозначно, якщо пов’язати їх з метричним тензором.

Нехай у метричному просторі заданий закон паралельного перенесення вектора

(33.1)

При переході від точки 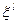до точки

,

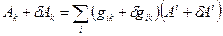-112-

тобто

Відкинемо доданок другого порядку мализни , тоді

Підставляючи сюди

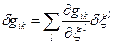
і вирази (33.1) і (33.2), одержимо

Далі підставимо

,

і тоді

а тому що і довільні

Останню рівність запишемо три рази змінюючи індекси

,

,

.

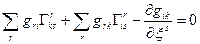Віднімемо від першого рівняння друге і третє, одержимо

,

.

Щоб визначити помножимо цю рівність на і просумуємо по . Тоді

,

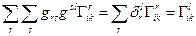і остаточно

-113-

(33.3)

Цей вираз називають символом Крістоффеля другого роду і позначають через

(33.4)

Вираз

(33.5)

називають символом Крістоффеля першого роду. Очевидно, що

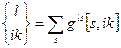(33.7)

Таким чином, ми познайомились з такими класами просторів:

1) декартовий (евклідовий)

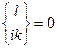
2) плоский (псевдо евклідовий)

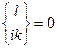
3) криволінійний

4) метричний

5) афінного зв’язку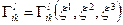

а) симетричний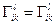

б) несиметричний

Всі наші міркування, всі результати і одержані формули не важко узагальнити на простори n вимірів. Особливий інтерес для фізики представляє чотирьохмірний простір Мінковського, інтервал в якому заданий формулою

Якщо прийняти

, , , ,

то метрика такого простору задана тензором

-114-

а сам простір Мінковського треба розглядати як чотирьохмірний, плоский, псевдо евклідовий простір.

У загальній теорії відносності основний є припущення про те, що реальний фізичний простір є чотирьохмірним метричним простором. Складені метричного тензора такого простору є функціями чотирьох координат, і вигляд залежить від розподілу речовини в просторі. Основна задача загальної теорії відносності і полягає у визначенні складових ,якщо відомий розподіл речовини.

Чоловік з дружиною піднялися на високу гору.

– Поглянь яка краса, який краєвид! Які чудові сади, хатини, річка!

Дружина зі злістю:

Якщо там така краса, то якого біса, ти заставив мене карабкатися на цю високу гору?

/З книги єврейського гумору/

34. Коваріантне диференціювання

Мішана похідна від тензора рангу N (N≥1) не є тензором. Однак можна утворити певні тензори, які відіграють роль звичайних похідних від тензорів.

Відзначимо, що закон паралельного перенесення

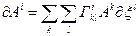
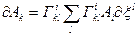
можна поширити на тензор довільного рангу. Проілюструємо це на прикладі мішаного добутку двох векторів , який є мішаним тензором другого рангу. При «паралельному перенесенні» такого добутку його складові зазнають зміни

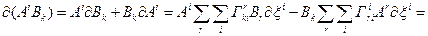
а, взагалі, для тензора другого рангу

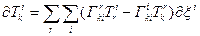
Закон паралельного перенесення тензора третього рангу матиме вигляд

-115-

Подібні формули можна записати і для тензорів вищих рангів.

Розглянемо для конкретності мішаний тензор другого рангу в точці 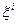. Перенесемо його паралельно в точку одержимо

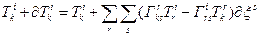
У точці тензор набуває значення

Різниця цих виразів

дорівнює

Вираз, що стоїть у дужці є тензором третього рангу і його називають коваріантною похідною тензора

/34.1/

Обмежуючись розглядом метричних просторів, ми можемо замінити коефіцієнти афінного зв’язку символами Крістоффеля другого роду.

Тоді

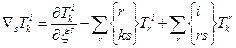/34.2/

Щоб одержати коваріантну похідну тензора довільного рангу треба до звичайної похідної додати додаткові члени. Кожному контраваріантному індексові відповідає доданок

/34.3/

а кожному коваріантному індексові – доданок

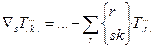/34.4/

Приклад. Коваріантною похідною тензора в тензор п’ятого рангу

Коваріантні похідні суми і добутку обчислюються за такими ж правилами як і звичайні похідні

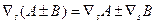/34.5/

-116-

/34.6/

Наприклад,

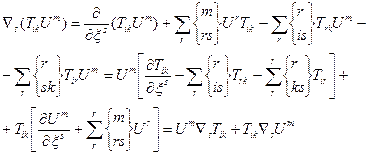
Легко переконатися, що коваріантна похідна від метричного тензора дорівнює нулеві

а цей вираз дорівнює нулеві /див. 33/. Таким чином,

/34.7/

При коваріантному диференціюванні добутку метричний тензор поводиться як стала величина

Доведемо, що коваріантна похідна тензора дійсно має тензорну розмірність. Для цього використаємо рівність /32.10/

Помножимо її на і просумуємо по k

Звідси

/34.8/

-117-

Продиференціюємо по рівність

Підставимо сюди /34.8/ і пере позначимо індекси в останній групі доданків

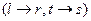
Тут

отже,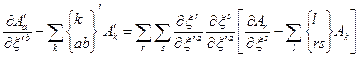

Звідси зрозуміло, що вираз

перетворюється як коваріантний тензор другого рангу. Аналогічним чином можна показати тензорний характер коваріантних похідних від тензорів вищих рангів.

Для декартового і косокутного просторів, коли , символи Крістоффеля дорівнюють нулеві і коваріантні похідні збігаються зі звичайними. У випадку скалярного поля звичайна похідна в коваріантним тензором першого рангу. 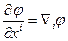Власне тому для оператора коваріантної похідної ми зберегли символ набла – оператор коваріантної похідної в узагальненням оператора набла.

-122-

Приклад 2. Сферичні координати

, ,

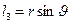
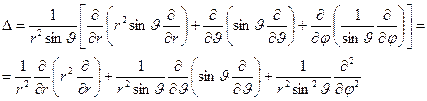
Приклад 3. Параболічні координати зв’язані з декартовими системою співвідношень

, ,

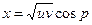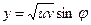Знайдемо оператор Лапласа в параболічних координатах.

Компоненти метричного тензора, як показують обчислення дорівнюють

, , , ,

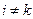
Звідси

, ,

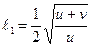а оператор Лапласа дорівнює

Виведемо ще іншу, еквівалентну /35.9/, формулу для оператора Лапласа. Приймаючи ми маємо

і остаточно

/35.11/

Познайомимось ще з ротором векторного поля в криволінійних координатах. Як ми показали в 30, різниця

-123-

є коваріантним антисиметричним тензором другого рангу, тобто псевдовектором. Власне цей псевдовектор, компоненти якого дорівнюють

, ,

є ротором векторного поля

/35.12/

Компоненти вектора R можна записати за допомогою символа e який зводиться так:

якщо два індекси однакові,

якщо i,j,k є парною перестановкою чисел 1,2,3,

якщо i,j,k є непарною перестановкою чисел 1,2,3.

Тоді

/35.13/

Дійсно, для i=1 ми маємо

Аналогічно одержуються вирази для R² і R³.

Те, що створюється ціною найбільших зусиль, повинно виглядати як таке, що створене швидко, майже без зусиль, з усією легкістю, наперекір правді.

Мікеланджело

36. Геодезичні лінії

Геодезичною лінією називається лінія найкоротшої віддалі в просторі криволінійних координат. В евклідовому просторі геодезичною є пряма лінія. На початку сфери такими лініями є великі круги.

Довжина лінії, що з’єднкє точки p₁ і p₂ дорівнює

, /36.1/

де p – довільний параметр.

-124-

Екстремум функціонала

визначається рівнянням Ейлера-Лагранжа

У нашому випадку

, ,

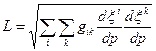тоді

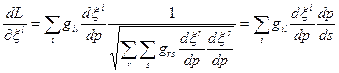
Варіаційний принцип запишеться

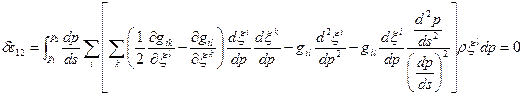
-125-

Симетризуємо першу групу доданків підінтегрального виразу

Рівняння геодезичних ліній одержується у вигляді

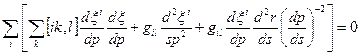
або, після перемноження на g^ls і сумування по l

/36.2/

Якщо за параметр прийняти дугу r=s, то , і

Дата добавления: 2015-05-24