Метричний тензор у косокутних координатах 4 страница

Розглянемо криволінійний простір, визначений координатами

тобто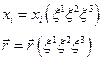

поруч з точкою М, визначеною радіусом-вектором , розглянемо нескінченно близьку точку з радіусом-вектором . Тоді

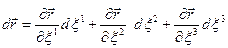/28.4/

порівняємо цей вираз з формулою

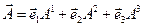
І, зокрема з формулою

Де 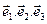- масштабні вектори косокутної системи, - контраваріантні складові вкктора 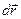. У рівності /28.4/ ми можемо вважати контраваріантними складовими вектора .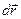

Тоді
можна інтегрувати як масштабні вектори в криволінійній системі координат

На відміну від косокутної системи часткові похідні є змінними величинами, тому

-кожній точці криволінійного простору можна поставити у відповідність

-95-

косокутну систему. Визначену масштабними векторами . Таку косокутну систему називають локальною або репером.

Нарисуємо координатні поверхні і координатні лінії, що відповідають точці М криволінійного простору. Нехай точка лежить на координатній лінії , тоді

У нашому конкретному випадку / точка знаходиться на лінії

І тому

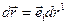
-вектори 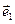і 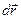колінеарні, вектор 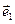є дотичним до координатної лінії . З другого боку

Де - довжина дуги , тому

вираз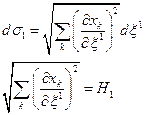

називають коефіцієнтом Ламе. Враховуючи, що

одержимо

Взагалі: масштабний вектор 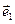є дотичним до координатної осі , його довжина дорівнює коефіцієнтові Ламе

За аналогією з теорії косокутних координат введемо луальні вектори в криволінійному просторі. Будемо виходити з формули

-96-

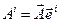
Приймаючи , ми одержуємо

З другого боку

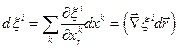
Порівнюючи дві останні рівності маємо

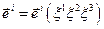
Легко переконатися, що як і для косокутних координат

дійсно

Тому що незалежні координати, похідна і дорівнює символу Крон екера.

Зауважимо, що вектор 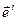- перпендикулярний до поверхні 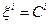. Це випливає з загальних властивостей градієнта скалярної функції/ див, 6/

29. матричний тензор в криволінійних координатах

Повернемося до формули

І згадаємо. Що величини є контраваріантними складовими вектора 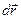у локальній системі координат, визначеній масштабними векторами . Коваріантні складові вектора визначається рівністю

Розкриємо скалярний добуток 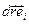в декартові системі

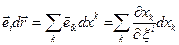
-97-

І врахуємо, що

Тоді /29.1/

Введемо позначення

/29.2/

Формула /29.1/ визначає операцію опускання індекса у контраваріантного вектора

/29.3/

Отже, величини треба інтерпретувати як коваріантні складові метричного тензора.

Таким чином. Ми ввели коваріантний метричний тензор у криволінійному просторі.легко бачити, що /29.2/ формально збігається з означенням метричного тензора в косокутному просторі

У випадку ортогональної криволінійної системи

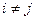
Приклад І. знайдемо компоненти метричного тензора для циліндричної системи координат.

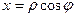
Маємо

-98-

.

Приклад 2. Компоненти метричного тензора для сферичної системи координат

, , ,

, , .

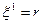Нескладний підрахунок дає:

,

,

,

,

,

.

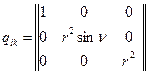Приклад 3. Знайдемо компоненти метричного тензора для координат поверхні тора

Координати поверхні тора пов’язані з декартовими за допомогою таких співвідношень:

,

,

,

Приймаючи

, , ,

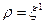маємо

-99-

,

,

,

,

,

.

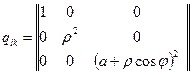Контраваріантні складові метричного тензора визначимо за формулами:

, /29.6/

тобто

. /29.7/

Як і в теорії косокутних координат, коваріантний метричний тензор зв’язаний з контраваріантним відомим співвідношенням:

. /29.8/

Справедливість цієї формули очевидна з такого ланцюга рівностей:

-100-

Зокрема, якщо криволінійна система ортогональна співвідношення між ко- і контраваріантними складовими метричного тензора істотно спрощуються. Наприклад, при

,

,

і взагалі

, .

У випадку ортогональної системи дуальний базис в ортогональним подібно як і базис . Приймаючи в /29.8/ маємо

,

, , ,

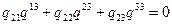і взагалі

, .

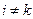Приклад 1. Матриця контрваріантного метричного тензора для циліндричної системи координат має вигляд

,

що можна перевірити безпосередньо

,

,

,

-101-

,

,

.

Приклад 2. Для сферичної системи координат

.

Зафіксуємо точку криволінійного простору і розглянемо в цій точці вектор 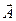. Його ко- і контраваріантні складові визначені формулами

, ,

.

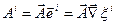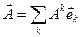Перемножуючи останню рівність на , одержимо

,

і аналогічно

.

Таким чином, відомі правила опускання і піднімання індексів справедливі і в криволінійному просторі.

Нехай задане векторне поле .

-102-

Ми можемо говорити про ко- і контраваріантні складові вектора 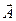в різних точках простору. При переході від точки до точки складові вектора змінюються:

а) за рахунок зміни вектора при переході від однієї точки простору до іншої;

б) за рахунок зміни репера /масштабних векторів /.

Рис. 77

Всі формули теорії косокутних координат залишаються правильними і для криволінійних просторів тільки тоді, коли мова йде про одну і цю ж точку простору.

В розв’язуванні проблем дослідник укріплює свої сили, знаходить нові методи і нові точки зору, відкриває більш широкі і вільні горизонти.

Д.Гільберт

30. Тензори в криволінійних просторах

Перейдемо від криволінійної системи /стара система/ до системи /нова система/, тоді

, /30.1/

, /30.2/

Ми записали, по суті, закон перетворення контраваріантних складових вектора 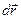при переході від однієї криволінійної системи до іншої. За таким же законом повинні перетворюватися контраваріантні складові будь-якого вектора 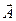, отже,

, /30.3/

. /30.4/

-103

Щоб знайти закон перетворення коваріантного вектора, розглянемо скалярну функцію . Зміна при нескінченно малому переміщенні дорівнює

. /30.5/

Ліва сторона /30.5/ є інваріантом, отже мусить бути коваріантним вектором. Закон його перетворення має вигляд

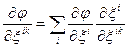. /30.6/

Цей же закон справедливий і для довільного коваріантного вектора

, /30.7/

і, очевидно,

. /30.8/

Одержані формули нагадують відомі закони перетворення з теорії косокутних координат

, ,

, .

Таким чином, можна вважати, що

,

, /30.9/

однак, тепер коефіцієнти і вже не є сталими

,

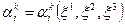. /30.10/

-104-

Легко переконатися, що залишаються справедливими формули, які зв’язують коефіцієнти і :

.

Приклад. Переконаємось, що скалярний добуток ко- і контраваріантного векторів є інваріантом і в криволінійному просторі. Ми маємо:

Формули /30.3/ - /30.4/ і /30.7/ - /30.8/ є, по суті, означенням контра- і коваріантного векторів у криволінійних просторах, тобто є означення тензорів першого рангу. Не представляє труднощів записати закони перетворення тензорів вищих рангів.

Компоненти тензорів другого рангу перетворюються за законами

,

,

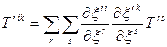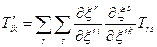, /30.11/

,

,

.

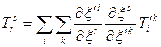У загальному випадку

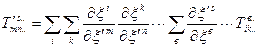. /30.12/

-105-

Ранг тензора можна понизити на дві одиниці за допомогою операції згортання

. /30.13/

Щоб довести це, у формулі /30.12/ проведемо сумування по індексах і

- ми одержали закон перетворення тензора рангу .

Очевидно вирази

,

тензорної розмірності не мають.

Розглянемо тепер мішані похідні і знайдемо їх трансформаційні властивості. Ми маємо

тобто

. /30.14/

Як видно, мішані похідні не є компонентами тензора. Однак, у випадку косокутних координат, коли

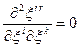
-106-

/старі і нові координати зв’язані лінійними співвідношеннями/, формула /30.14/ дає закон перетворення коваріантного тензора другого рангу /пор.§27/.

Цікаво відзначити, що різниця

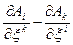
Є коваріантним антисиметричним тензором другого рангу /ротор у криволінійних координатах/. Дійсно, при переході до нової системи ми одержуємо закон перетворення тензора другого рангу

Зауважимо, що мішані похідні , і навіть їх різниця

не є тензорами, що легко перевірити аналізуючи трансформаційні властивості цих виразів.

Звичайно, причинні зв’язки слід встановлювати, виходячи з досвіду, але ми не повинні відмовлятися від обов’язку виправляти й доповнювати наше розуміння спостережуваних явищ подальшим міркуванням.

Б.Ріман

31. Метричні простори

Розглянемо дві нескінченно близькі точки в просторі декартових координат. Віддаль між ними визначається відомою формулою

. /31.1/

-107-

При переході до криволінійних координат

Дев’ять величин

, /31.2/

як відомо, називають коваріантними складовими метричного тензора, вони задають метрику криволінійного простору. Таким чином,

. /31.3/

Здійснимо зворотній перехід від криволінійної до декартової системи. Ми знову приходимо до формули

,

тобто добиваємось того, що метричний тензор переходить у символ Крон екера

.

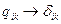Існують простори, в яких не можна ввести декартової системи координат. Класичним прикладом такого простору є двомірна поверхня сфери. Положення точки на сфері визначається двома кутами і .

-106-

Тоді

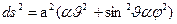
– квадрат диференціала дуги заданий як однорідна квадратична форма координат.

Подібні простори називаються метричними або рімановими. Таким чином, метричний простір задається дев’ятьма складовими метричного тензора

,

причому

Рис. 78

.

Якщо в метричному просторі можна ввести таку систему координат, для якої 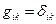, то ця система буде декартовою, а простір – евклідовим. З цієї точки зору, простір, визначений циліндричними координатами є евклідовим, тому що завжди можна перейти до декартових координат за відомими формулами

, ,

Евклідові простори є тільки класом метричних просторів.

Переконаємось, що поняття метричного тензора не зв’язане з існуванням декартової системи координат. Нехай простір метричний

Здійснимо перетворення координат , тоді

,

.

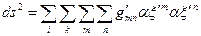З другого боку

.

Порівнюючи обидва вирази для маємо

-107-

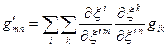(31.4)

– перетворюється як коваріантний тензор.

Контраваріантний метричний тензор вводиться в метричному просторі за допомогою співвідношень

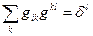(31.5)

Звідси випливає, що

,

де

.

Дата добавления: 2015-05-24